Knobelfrage Radius ermitteln?
Hallo,
ich muss den Radius des kleinen gelben Kreises berechnen. Den Pythagoras habe ich schon probiert, leider erfolglos. Hat hier jemand einen Vorschlag bzw. sogar die Lösung?
Danke!

Haste ma die Radien parat? Die Maße
Hi, ich habe ein Bild von der Aufgabe darunter gestellt. Die Radien sollten darin zu sehen sein, andernfalls lade ich das Bild erneut hoch.
5 Antworten
Eine Seite des Dreiecks zwischen den Mittelpunkten ist 6, die anderen beiden 4+x und 2+x. Betrachtet man die Höhe dieses großen Dreiecks, ist diese je eine Kathete der rechtwinkligen Dreicke, aus denen das große Dreieck besteht.
Deshalb gilt ja (2+x)^2 = p^2 + h^2 und (4+x)^2 = q^2 + h^2
Löst man beide nach h^2 auf und setzt sie gleich erhält man
(4+x)^2 - q^2 = (2+x)^2 - p^2
Hier müsstest du nur noch q und p separieren und durch 6 ersetzen (p + q = 6) und nach x auflösen
Das Problem ist übrigens auch als Sangaku bekannt, hierzu kannst du Mal nach Lösungsansätzen im Internet schauen.
Stimmt, hab ich tatsächlich nicht gesehen, dass alle drei eine gemeinsame Tangente besitzen, aber wie würdest du es lösen?
Das ist ein beliebtes Thema.
Du brauchst nur das:

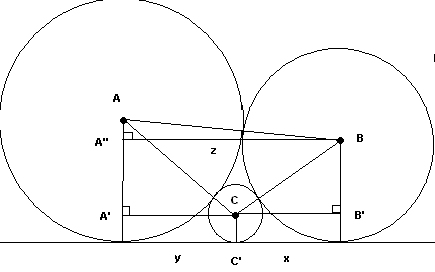
AB ist die Summe der beiden Radien.
AA'' ist nur die Differenz der beiden Radien, womit du ein rechtwinkliges Dreieck hast aka Zeit für den Satz des Pythagoras: (AB)² = (AA'')² + (A''B)²
Dadurch ist dann der gesuchte Radius c wieder gegeben durch den Satz des Pythagoras: (BC)² = (BB')² + (B'C)² und (AC)² = (AA')² + (B'C)²
Die drei Gleichungen reichen um es zu finden.
Ein nettes Video dazu ist: https://www.youtube.com/watch?v=i0dZukEw1JY
Kontrollergebnis (c ist der gesuchte Radius und a und b sind die gegebenen Radien):
c = ab / [sqrt(a) + sqrt(b)]²
c = 0,6862915010...
Also. Doch. Satz des Phytagoras funktioniert.
Wäre halt nur
(2+x)² + (4+x)² = 36
Jetzt nur noch nach x auflösen wie immer
Binomische Formeln anwenden, und dafür sorgen dass man die pq-Formel anwenden kann:
4+4x +x² + 16+ 8x + x² = 36
2x² +12x +20 = 36 | :2 |
x² + 6x + 10 = 18 | -18
x² + 6x -8 =0 Pqfromel
x1= 1,12311
x2= -7,12311 (egal)
Und wenn man jetzt x1 für x einsetzt bekommt man da 36, bzw 6 raus.
(2+1,12311)² + (4+1,12311)² = 36
Das Problem ist nur, dass das kein rechtwinkliges Dreieck ist. Da funktioniert der Satz des Pythagoras nicht.
@Levitikus1337: Leider falsch.
Pythagoras ist nur anwendbar bei rechtwinkligen Dreiecken!
Den Pythagoras habe ich schon probiert
aber wohl nicht oft genug :)
- Ziehe je eine Waagrechte w₁ durch den gelben Mittelpunkt und eine w₂ durch den roten.
- Ziehe je eine Senkrechte s₁ durch den roten Mittelpunkt und eine s₂ durch den blauen.
Sei r der gesuchte Radius. An w₁ und s₁ findest Du ein rechtwinkliges Dreieck, dessen waagrechte Unterseite sich in Abhängigkeit von r berechnen lässt. Dasselbe geht an w₁ und s₂. Die Summe dieser beiden Unterseiten findest Du im großen Dreieck über w₂. Jetzt nur noch r ausrechnen und fertig!
Mit 3x Pythagoras und etwas Umformerei geht es.

Die blaue und die gelbe Linie kann man mit den unteren beiden Dreiecken durch die gegebenen Radien und den Radius r des gelben Kreises (rote Linie) ausdrücken. Die Resultate addiert man und bekommt die Länge der grünen Linie in Abhängigkeit von r. Damit kann man aus dem oberen Dreieck dann r berechnen.
r = 0,68629…

Das dürfte nicht reichen, p + q = 6 erlaubt keine Aussage über q^2 - p^2.
Dein Ansatz gilt abgesehen davon für jeden Kreis, der wie der gelbe die anderen beiden Kreise berührt. D.h., du hast nicht benutzt, dass die drei Kreise eine gemeinsame Tangente haben.