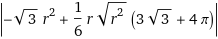Mathe Kreise Schnittfläche Flächeninhalt?

Zeichne zwei Kreise mit gleichem Radius, von denen jeder durch den Mittelpunkt des anderen geht. Berechne die Schnittfläche der beiden Kreise.

Brauche hilfe mit dieser Aufagbe

danke schonmal :)

Answer 1

[LORDderANALYSE]

Stelle die beiden Kreise einfach als Funktionen dar:

Kreis 1: f(x) = sqrt(r² - x²)
Kreis 2: f(x) = -sqrt(r² - x²) + r

("r" steht für den Radius)

Dann ist die Schnittfläche, dass Integral beider Funktion von den Schnittpunkt zum anderen Schnittpunkt von einander abgezogen dein Flächeninhalt.

Zuerst berechnen wir die Schnittpunkte:

Schnittpunkte: sqrt(r² - x²) = -sqrt(r² - x²) + r | +sqrt(r² - x²)
Schnittpunkte: 2 sqrt(r² - x²) = r                | :2
Schnittpunkte: sqrt(r² - x²) = r / 2              | ()²
Schnittpunkte: r² - x² = r² / 4                   | -(a² / 4 + x²)
Schnittpunkte: x² = (4 r² - a²) / 4
Schnittpunkte: x² = (3 r²) / 4                    | sqrt()
Schnittpunkte: x = sqrt(3) / 2 r, x = -sqrt(3) / 2 r + r

Dann nehmen wir die Integrale:

$A=\left|\int_{-\frac{\sqrt{3}}{2}\cdot r}^{\frac{\sqrt{3}}{2}\cdot r}\sqrt{r^2-x^2}dx-\int_{-\frac{\sqrt{3}}{2}\cdot r}^{\frac{\sqrt{3}}{2}\cdot r}-\sqrt{r^2-x^2}+r\ dx\right|$

Und das ist dann auch dein Flächeninhalt.

Das kannst du jetzt noch weiter vereinfachen zu:

(das ist deine Schnittfläche)

Da:

Woher ich das weiß: Studium / Ausbildung