Ist es möglich ein Programm zu entwickeln, das alle mathematische Beweise machen kann?
9 Stimmen
6 Antworten
Um Beweise zu führen, bedarf es Intuition - KI hat keine Intuition…
Es gibt schon lange https://de.wikipedia.org/wiki/Maschinengest%C3%BCtztes_Beweisen. Heute mit Programmen wie Coq oder Lean.
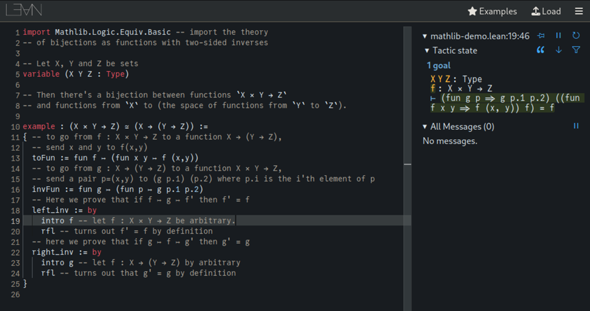
Sieht in etwa so aus (Quellcode aus den Beispielen von Lean):

Das Problem damit, alles zu beweisen, ist, dass es erstens viel zu viel gibt, was man beweisen könnte und vieles davon auch überhaupt keine Anwendung hat. Es braucht etwas, was da durch sortiert und diesen Prozess leitet.
Ich denke, in der Zukunft werden sich diese Tools weiterentwickeln. ChatGPT z. B. kann auch schon manchmal Beweise zu einer Textbeschreibung liefern. So etwas mit WolframAlpha und einem Theorem-Prover zu verbinden klingt schon echt stark.
Dann liegt es aber immer noch an Menschen, sicherzustellen, dass diese Prozesse funktionieren, die richtigen Ziele haben und auf Basis unserer Systeme (was ist "Mathematik" überhaupt?) und Werte arbeiten.
Nein. Schon die Prädikatenlogik 1. Stufe ist nicht entscheidbar, ebensowenig die Arithmetik.
Definitiv nein. Das ist durch den Gödelschen Unvollständigkeitssatz bewiesen.
Der Gödelsche Unvollständigkeitssatz besagt, daß die Arithmetik nicht vollständig axiomatisierbar ist, d.h. daß es immer wahre Sätze der Arithmetik gibt, die nicht beweisbar sind. Dies würde aber noch nicht ausschließen, daß es ein Programm geben könnte, daß alle *beweisbaren* Sätze auch beweist. Auch dies geht aber nicht, da die Arithmetik nicht nur nicht vollständig axiomatisierbar ist, wie Gödel gezeigt hat, sondern auch nicht entscheidbar ist, wie Alonzo Church gezeigt hat. Würde die Frage lauten: "Ist es möglich, ein Programm zu entwickeln, das alle *wahren* mathematischen Sätze beweist?", dann hättest Du recht: Dies geht schon wegen Gödel nicht, da es wahre mathematische Sätze gibt, die nicht beweisbar sind. Ich verstehe die Frage: "... das alle mathematischen Beweise machen kann?" aber als: "... das alle *beweisbaren* mathematischen Sätze beweisen kann?" Auch ein solches Programm kann es nicht geben, aber das hat nicht Gödel gezeigt, sondern Church.
Eher mehrere Programme für mehrere Probleme