Ich bräuchte hilfe, bei dem aufstellen der Normalen in der nulstelle?

Gegeben ist die Funktion f(x) = ln(0, 5x + 3) . Bestimmen Sie die Definitionsmenge von f, skizzieren Sie den Graphen von f und stellen Sie die Gleichung der Normalen in der Nullstelle auf.

Danke schonmal vorab

Answer 1

[mihisu]

Da die Gleichung der Normalen in der Nullstelle gefragt ist, ist es doch zunächst wohl relevant, wo sich diese Nullstelle befindet.

• Berechne die Nullstelle x₀ der Funktion f. Löse dazu die Gleichung f(x) = 0, also die Gleichung ln(0,5x + 3) = 0, nach x auf.

Die Normale verläuft senkrecht/orthogonal/normal zur Tangente. Berechne also zunächst einmal die Tangentensteigung von f an der Stelle x₀. Dazu solltest du wissen, dass die Tangentensteigung gleich der ersten Ableitung an der entsprechenden Stelle ist.

• Berechne die Tangentensteigung von f an der Stelle x₀ mit Hilfe der Ableitung, also m[Tangente] = f′(x₀).

Wenn man die Steigung der Normale mit der Steigung der Tangente multipliziert, erhält man -1. Die Normalensteigung ist hier dementsprechend der negative Kehrwert der Tangentensteigung.

• Berechne die Tangentensteigung mit m[Normale] = -1/m[Tangente].

Du hast nun die Steigung der Tangente gegeben. Außerdem weißt du, dass die Normale durch die Nullstelle verläuft, also durch den Punkt (x₀ | 0) verläuft. Dementsprechend erhält man als Geradengleichung in Punkt-Steigungs-Form...

• Die Gleichung der Normalen ist durch y = m[Normale] ⋅ (x - x₀) + 0 gegeben, wobei das „+ 0“ keine Auswirkungen hat, man also auch einfach y = m[Normale] ⋅ (x - x₀) mit den zuvor berechneten Werten für m[Normale] und x₀ angeben kann.

====== Lösungsvorschlag zum Vergleich ======

Answer 2

[DerRoll]

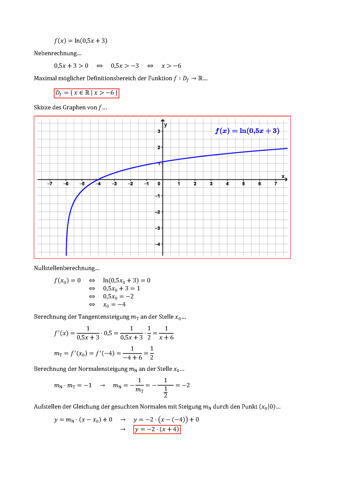
Berechne den Wert Ableitung (= Steigung der Tangenten) m an der Nullstelle x0 von f. Wenn eine Gerade g(x) = m*x + b die Steigung m hat, so hat die zu g senkrechte Gerade die Steigung -1/m. Überlege dir diese Tatsache in einem Koordinatensytem. Das sollte Stoff der 8. Klasse sein. Den y-Achsenabschnitt der Normalen kannst du dann berechnen indem du die Gleichung f(x0) = -x0/m + c nach c auflöst.