Was ist bei dieser Aufgabe zu tun?
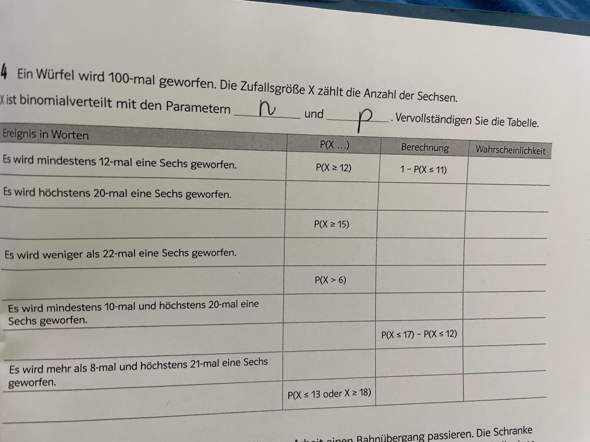
So das ist die Aufgabe und ich weiß gar nicht, was dort zu tun ist. Deswegen bräuchte ich dringend Hilfe. Weiß jemand wie man überhaupt anfängt und kann mir jemand einen Tipp geben sodass ich die Aufgaben problemlos lösen kann?
LG
2 Antworten
(A)
Über die Wahrscheinlichkeitsrechnung beim Würfeln findest Du hier etwas.
https://www.poissonverteilung.de/binomialverteilung.html
https://www.univie.ac.at/psy-methoden-tutorium/ws08/ws08_tut06_bsp03(lsg).pdf
Die Formel, die qualle930 genannt hat, wird dort auch erklärt, es ist die Wahrscheinlichkeitsfunktion der Binomialverteilung.
Was Du bei Deiner Aufgabe für die Fragen mit P(X ≤ k) oder P(X ≥ k) benötigst, ist aber die Verteilungsfunktion der Binomialverteilung.
Nützlich ist diese Formel:
P(X ≥ k) = 1 − P(X ≤ k−1)
https://www.maths2mind.com/schluesselwoerter/verteilungsfunktion-binomialverteilung
(B)
Hier ist ein Online-Rechner für diese Art von Aufgaben...
http://www.juergenmeisel.de/schule_iv_themen/schule_iv_js/php/bin_vert/binom_vert.php
...und hier ist noch einer:
https://matheguru.com/stochastik/binomialverteilung.html
Was Du in das Formular eingeben mußt:
n = 100 (Die Gesamtzahl der Versuche)
k = ... (Wie viel mal die Sechs dabei sein soll: mindestens 12 mal, mindestens 20 mal usw.)
p = 0.1666666666666667 (d.h. 1/6, die Wahrscheinlichkeit für eine Sechs bei einem Würfel)
Wo die Lösung angezeigt wird, mußt Du auswählen, welche Du benötigst. Bei Dir sind die Lösungen für ≥ oder ≤ gefragt.
- P(X = k) ["genau"],
- P(X ≤ k) ["höchstens"]
- P(X ≥ k) ["mindestens"]
Entweder du berechnest es mit der Formel händisch oder mit dem Taschenrechner.
Der Fall P(X=k) ist bei den hier gestellten Aufgaben aber nicht dabei.
Die benötigte Formel ist etwas komplizierter. Ich weiß nicht, ob heutige Taschenrechner sie fertig eingebaut haben.
http://www.juergenmeisel.de/schule_iv_themen/schule_iv_js/php/bin_vert/bin_vert.gif
Die CDF Funktion haben normalerweise die Taschenrechner. Rein theoretisch könnte man es ja auch mit PFD ausrechnen, ist halt ein viel größerer Aufwand
So, die Dinger können das. OK, meinen letzten Taschenrechner verwendete ich in den 1980er Jahren. Stimmt, der Aufwand wäre unangenehm und gleichzeitig das Risiko, sich zu vertun. Ich programmiere solche Sachen heute mit Perl oder mit Maxima, da kann ich genau nachvollziehen, was ich gemacht und ggf. falsch gemacht habe.
Formel:
https://matheguru.com/images/latex//306381a2142349cf40135dd85e181b6f.svg