Habe ich mich hier verrechnet??
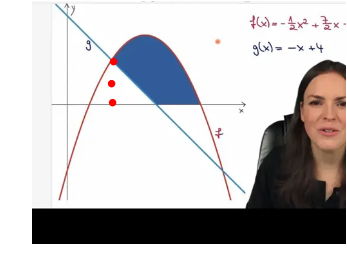
Bekomme ein anderes Ergebnis raus als sie. Da ich einen anderen rechenweg habe, kann ich nicht überprüfen, ob und wo ich einen Fehler gemacht habe. Was bekommt ihr bei der Aufgabe raus? Mal soll die blaue Fläche berechnen



3 Antworten
Die Fläche zwischen der Parabel f(x) und der x-Achse bestimmt man mit dem Integral. Dieses sei F(x). Integriert man f(x), erhält man
F(x)=-1/6x^3+7/4x^2-3x+c
c ist eine Konstante, die noch zu bestimmen ist.
Probe: Differenzierst du F(x) muß f(x) rauskommen. Dies ist der Fall.
Um c zu ermltteln, bestimmen wir zunächst den kleineren Schnittpunkt von f(x)=g(x). Dies ergibt 2.
Wir legen fest: F(2)=0
Dies ergibt c-1/3=0. Somit können wir c bestimmen mit c=1/3.
Die zweite Nullstelle f(x) ergibt 6. Die Nullstelle von g(x) ist bei x=4. Wir ziehen dann von F(6) die Dreiecksfläche wie folgt ab:
F(6)-1/2×(4-2)×f(2)=22/3
22/3 ist die gesuchte Fläche.
Also ich hätte es spontan wie folgt gemacht:
1. Schnittpunkt von g und f berechnen
2. Nullstelle von g berechnen
3. Erste Teilfläche - Integral von f(x) - g(x) mit den Grenzen x vom Schnittpunkt bis zur Nullstelle von g
4. Zweite Teilfläche - Integral von f(x) mit den Grenzen von der Nullstelle von g bis zur Nullstelle von f
5. Ergebnis - die Flächen einfach addieren
Würde mich interessieren, ob meine Lösung auch gehen würde ;)
EDIT: Hab's mal in Mathcad durchgerechnet:


Dein Ergebnis stimmt mit dem Video überein 👍🏻Hast du eine Idee wie man die weiße Fläche über der x Achse aber innerhalb der Parabel berechnet?

berechne den Schnittpunkt xS
und Summiere links unter der Parabel plus rechts unter der Geraden