Gleichung nach X umstellen, Wendepunkte berechenen?
Hallo ich möchte gerne die Wendepunkte berechnen. Dafür muss ich die 2 Ableitung nach X auflösen. Wie kann ich
0= 1/2x² + 2x
nach X umstellen?
Gibt es da eine Formel für?
Hab die
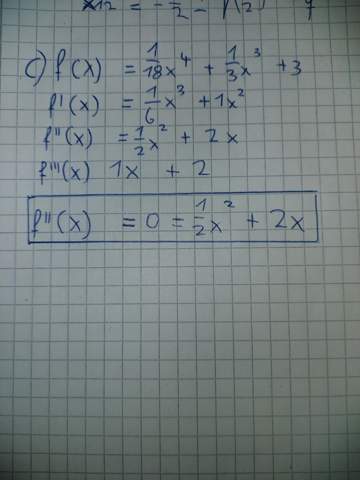
Gleichung nochmal als Bild reingepackt.
3 Antworten
Vom Fragesteller als hilfreich ausgezeichnet
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Gleichungen, Mathematik
Guten Morgen.
Du hast einen Fehler bei den Ableitungen:
f(x) = (1/18)x^4 + (1/3)x^3 + 3
f'(x) = (2/9)x^3 + x^2
f''(x) = (2/3)x² + 2x
Jetzt einfach gleich 0 setzen, dafür bietet sich in diesem Fall der Satz vom Nullprodukt an:
(2/3)x² + 2x = 0
x((2/3)x + 2) = 0
x = 0
......
(2/3)x + 2 = 0 | - 2
(2/3)x = -2 | : (2/3)
x = -3
Du hast also zwei Wendepunkte. Dafür musst du nun einfach nur noch die x Koordinaten in die ursprüngliche Funktion einsetzen:
f(0) = 0 + 0 + 3
f(0) = 3
.............
f(-3) = (81/18) - (27/3) + 3
f(-3) = (27/6) - (54/6) + 3
f(-3) = 4,5 - 9 + 3
f(-3) = -1,5
Das ergibt die beiden Wendepunkt (0|3) und (-3|-1,5).
Woher ich das weiß:Studium / Ausbildung – Diplom Wirtschaftsinformatiker
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Gleichungen, Mathematik
Rechenfehler bei der 1. Ableitung: nicht 1/6 x^3, sondern 4/18 x^3…
Woher ich das weiß:Studium / Ausbildung – PhD Analytische & Algebraische Zahlentheorie
•2 nehmen, dann P-Q Formel anwenden
Lieben dank für deine schnelle Antwort. Dann hätte ich ein X1 und ein X2 raus, wie mache ich dann weiter? Ist es egal welchen Wert ich dann nehme?