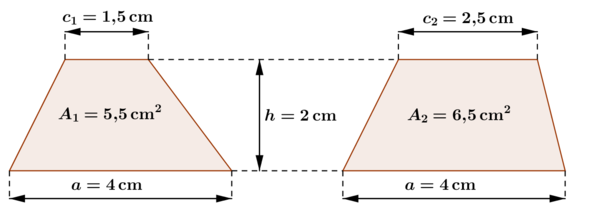
Flächeninhalt eines Trapez mit Seite a und Höhe berechnen?
Ist es möglich, mithilfe der gegebenen Höhe (h) und der Seite a (a) eines Trapezes, den Flächeninhalt oder wenigstens die Seite c (c) zu berechnen. Gibt es irgendeinen Satz oder einen weiten Umweg, um diesen zu berechnen?
Danke für schnelle AntwortenCoernerbrot
6 Antworten
Falls nur a und h gegeben sind, ist das Trapez natürlich gar noch nicht festgelegt, also auch nicht sein Flächeninhalt. Man braucht wenigstens eine weitere (geeignete) Größe, beispielsweise die Länge der zu a parallelen Seite c.
Nein ist es nicht, c ist ja komplett unabhängig von a und h. C könnte ja auch einen Millimeter länger sein, somit wäre der gesamte Flächeninhalt verändert. Das spricht natürlich dafür, dass man den Flächeninhalt damit auch nicht berechnen kann:)
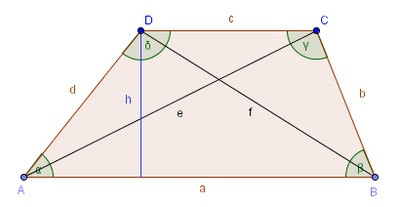
Der Flächeninhalt des Trapezes ist 0,5*(a+c)*h.Man benötigt also drei Größen, um den Flächeninhalt zu bestimmen. Das können auch drei andere Größen des Trapezes sein - aber 3 Stück müssen es in jedem Fall sein. Damit ist aber nur der Flächeninhalt festgelegt. Es gibt beliebig viele Trapeze, die diesen Flächeninhalt besitzen, denn wenn man die Seite c auf einer Parallelen zu a im Abstand h beliebig verschiebt, erhält man lauter Trapeze mit dem selben Flächeninhalt.
Um ein Trapez nun auch noch in der Form festzulegen, benötigt man eine vierte Größe, entweder einen der WInkel oder eine weitere Seite.
Mit den von dir gegebenen Voraussetzungen, a und h bekannt, kann man also gar nichts berechnen - auch nicht über einen sehr langen Weg
Nur mit der Angabe von a und h (und ohne Winkelangaben) ist das Trabez nicht vollständig definiert, somit kannst du auch nichts berechnen
Nein, alleine durch a und h ist das Trapez noch nicht eindeutig bestimmt.
Siehe auch: Bild im Anhang
Für gleiches a und gleiches h gibt es Trapeze mit unterschiedlichem Flächeninhalt und unterschiedlichem c.