Der Graph einer Polynomfunktion f vom Grad 4 hat einen Hochpunkt im Koordinatenursprung?
Der Graph einer Polynomfunktion f vom Grad 4 hat einen Hochpunkt im Koordinatenursprung. Im Wendepunkt W(1/-1) ist die Tangente parallel zu ersten Achse. Wie kann ich die Termdarstellung ermitteln, kann mir da wer helfen?
4 Antworten
Die Funktion geht durch den Koordinatenursprung. Weil sie auch einen Hochpunkt dort hat hat sie also eine doppelte Nullstelle. Weiterhin geht sie durch (1/-1) und hat dort einen Wendepunkt. Was die "erste Achse" ist weiß ich nun nicht, das solltest du noch mal genau ermitteln. Aber damit hast du fünf Informaitonen für fünf unbekannte. Nun ans Werk.
Eigentlich ist es egal wie es "eigentlich heißt", frei nach Hilbert
https://de.wikipedia.org/wiki/Hilberts_Axiomensystem_der_euklidischen_Geometrie
Hilbert soll einmal gesagt haben, man könne statt „Punkte, Geraden und Ebenen“ jederzeit auch „Tische, Stühle und Bierseidel“ sagen; es komme nur darauf an, dass die Axiome erfüllt sind.
es muß nur klar sein was gemeint ist, und das war hier halt offensichtlich nicht der Fall, wenn zwei Mathematiker daran scheitern.
f(x)=ax⁴+bx³+cx²+dx+e
f'(x)=...
f''(x)=...
Hochpunkt im Ursprung:
f(0)=0
f'(0)=0
Wendepunkt W(1|-1) mit Tangente parallel zur x-Achse, also Tangentensteigung=0
f(1)=-1
f'(1)=0 Steigung der Wendetangenten
f''(1)=0 Wendepunktsbedingung
mit diesen 5 Bedingungen kannst du ein LGS mit 5 Gleichungen aufstellen und dann die Unbekannten a, b, c, d und e bestimmen
Die bedingungen habe ich schon alles aufgeschrieben aber ich bekomm dann 3 gleichungen heraus wie soll ich da die koeffizienten berechnen?
es gibt 5 Bedingungen, hab alle oben aufgeschrieben
mit f(0)=0 erhält man sofort e=0
mit f'(0)=0 erhält man d=0
diese beiden Werte kannst du dann direkt als d und e in die f(1)=-1 einsetzen
Das verstehe ich eh das dann d und e null sind aber wie werde ich die anderen variablen ausrechnen können wenn ich 3 gleichungen hab
f(1)=-1 => a+b+c=-1
f'(1)=0 => 4a+3b+2c=0
f''(1)=0 => 12a+6b+2c=0
dritte Gleichung minus zweite
zweite Gleichung minus 2x erste, dann ist c weg und man hat nur noch zwei Gleichungen mit a und b
Könntest du mir vielleicht den Vorgang mit den Zahlen aufschreiben , weil bei mir kommt irgendwie b=0 heraus und das stimmt nicht
dritte Gleichung minus zweite
erste Gleichung mal -2 plus zweite
8a+3b=0
2a+b=2
-------------
2a=-6
a=-3
b=8
Der Graph einer Polynomfunktion f vom Grad 4 hat einen Hochpunkt im Koordinatenursprung. Im Wendepunkt W(1/-1) ist die Tangente parallel zu ersten Achse. Wie kann ich die Termdarstellung ermitteln, kann mir da wer helfen?
Schau mal hier:
https://www.youtube.com/watch?v=b25InOh-AUk
(Was auch immer die "erste Achse" sein soll)
Die erste achse ist die x achse und da ist die steigung 0, sehr komisch, dass du sowas nicht gewusst hast
Weißt du, die Benennungen dieser Art sind durchaus unterschiedlich. Und es macht nebenbei keinen Sinn die die dir helfen wollen auch noch vor den Kopf zu stoßen.
f(x)=ax⁴+bx³+cx²+dx+e
f'(x)=4ax^3+3bx^2+2cx+d
f''(x)=12ax^2+6bx+2c
f(0)=0 --> e=0
f'(0)=0 --> d=0
f(1)=-1 = a+b+c (1)
f'(1)=0 = 4a+3b+2c (2)
f''(1)=0 =12a+6b+2c (3)
c eliminieren:
(3)-(2) --> 0 = 8a+3b (4)
(3)-2*(1) --> 2 = 10a+4b (5)
4*(5)-5*(4) --> 8=b ; a=-3
a und b in (1) --> -1=-3+8+c --> c=-6
f(x)=-3x^4+8x^3-6x^2
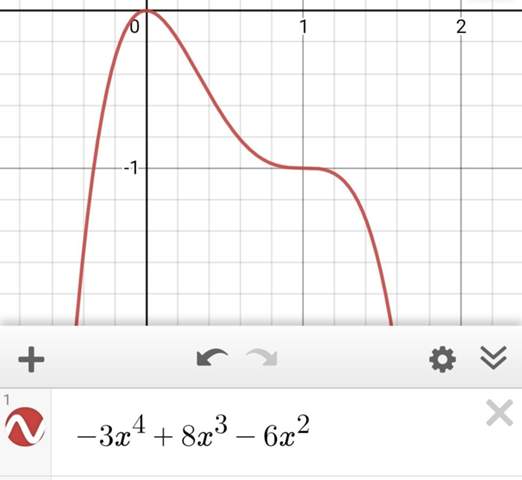
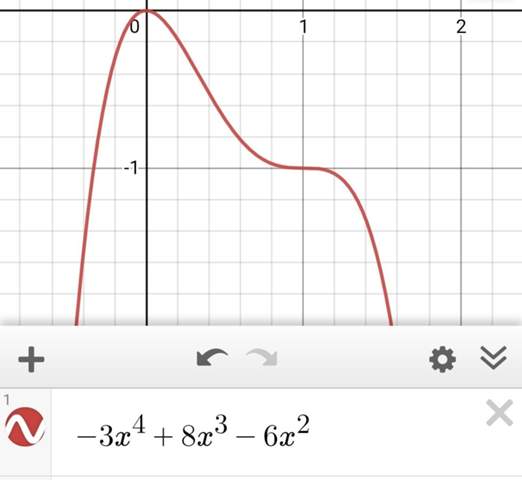
Die erste Achse ist die x-Achse.
:-)