cos(x)=-0,5 bestimme die x-werte im Intervall |0; 2π) wo das der fall ist?
Also in Bogenmaß. Ich habe jetzt mit dem Taschenrechner x1= 2,094 rausbekommen
Aber wir bekomme ich jetzt den anderen wert raus? Weil die funtion f(x)=cos(x) schneidet die gerade y=-0,5 ja noch in einem anderen punkt. Aber wie bekomme ich heraus bei welchem x-wert?
Danke schonmal
Naomi2002
3 Antworten
Sieh dir die Funktion an:
(blau: Kosinus, rot: -0,5. Um die Schnittpunkte geht es)
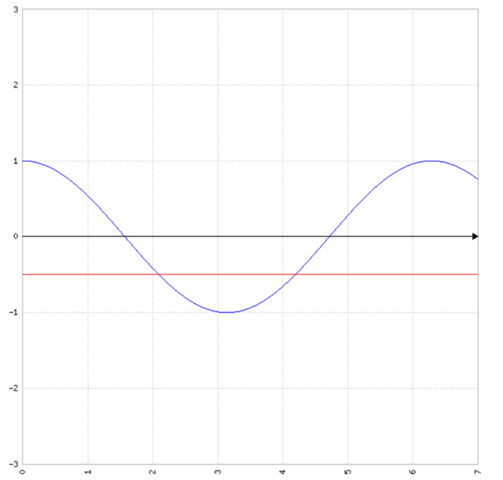
Man sieht, dass die Schnittpunkte symmetrisch zum Minimum des Kosinus (-1 bei x = pi) liegen müssen.
dein x1 von 2,094 ist also genau so weit von pi entfernt, wie dein x2.
Es gilt also: x2 = (pi-x1)+pi = 2pi-x1
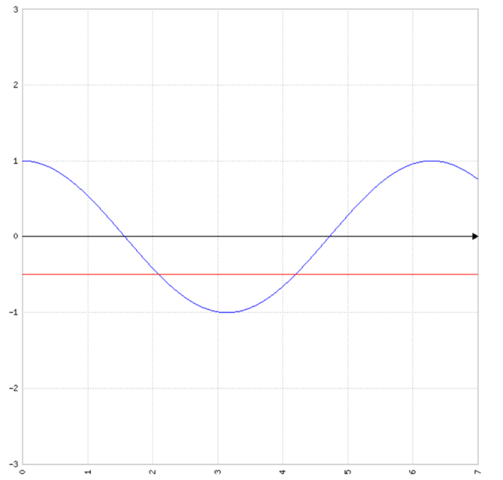
Dann teile den Wert 2,094 mal durch π und du bekommst raus:
cos( 2/3 • π ) = -0,5
Es gibt noch eine weitere Lösung, die der Taschenrechner dir aber nicht gibt. Siehe dir dazu die Cosiuskurve mal an, wann deren Wert wieder bei -0,5 ist.
Wie ist das Symmetrieverhalten der Cosinusfunktion? Wo sind Spiegelachsen?
Hallo Naomi,
am besten, du machst dir eine Skizze und findest die beiden Punkte dort. Dann wirst du wahrscheinlich sehr schnell sehen, wo der andere Punkt ist!
das habe ich schon gemacht, ich bin aber nicht darauf gekommen gewesen wie die punkte "von einanre abhängen"
Hast du denn auch die Kurve in den negativen x-Bereich weiter gezeichnet?
Ok, super! :)
Trotzdem noch zur alternativen Herangehensweise: Zu x1=2,094 ist auch
x2=-x1=-2,094
wieder eine Lösung, denn der Kosinus ist eine achsensymmetrische Funktion.
Möchtest du die entsprechende Lösung im Bereich zwischen 0 und 2pi, dann addiere 2pi:
x2'=x2+2pi=-2,094+2pi
ah danke du hast mir sehr geholfen!!! Jatzt habe ich es endlich verstanden!!!!