Es gibt nur 1 Wahrscheinlichkeit - oder?
Wenn ich z.B Roulette spiele, liegt die Wahrscheinlichkeit auf Rot bei 48,65%.
Aber ich habe das Gefühl, dass sehr viele Menschen noch glauben, dass die Wahrscheinlichkeit zurückgeht, wenn es um mehrere Gewinne hintereinander geht. Also beispielsweise 20x hintereinander auf rot ist nicht mehr 48,65%.
Aber rein logisch betrachtet gibt es doch nur eine Wahrscheinlichkeit, sodass die Wahrscheinlichkeit 100000x hintereinander auf rot zu landen, 48,65% liegt. ist das korrekt?
weil dass es auf rot fällt, hat doch keinen Einfluss auf das vorherige Ergebnis
8 Antworten
Ja, das ist korrekt.
Jedes einzelne Spiel ist unabhängig von allen vorherigen.
Das sind unabhängige Ereignisse, genau wie z.B. beim Würfeln.
Lehrsatz:
Die Eintreffwahrscheinlichkeit eines zufälligen Ereignisses ist unabhängig von den vorhergegangenen gleichen zufälligen Ereignissen.
weil dass es auf rot fällt, hat doch keinen Einfluss auf das vorherige Ergebnis
Fast, aber korrekt müsste es heißen:
weil dass es auf rot fällt, wird doch nicht durch das vorherige Ergebnis beeinflusst
Das unterstelle ich grundsätzlich, wenn im mathematischen Sinn von "zufällig" die Sprache ist.
Die Frage ist halt :
- Gehts dir um die echte Einzelwahrscheinlichkeit?
- Oder die Wahrscheinlichkeit 10.000 + mal HINTEREINANDER IMMER Rot zu kriegen?
Sind halt zwei unterschiedliche Dinge. Im Ersteren Fall bleibt es halt bei den 48,65%. Bei einer Kette sinkt die Wahrscheinlichkeit natürlich in der Gesamtheit, dass es so eintritt.
aber wieso sinkt es? es ist doch immer 48,65 bei jedem dreh
das "es" was sinkt , ist nicht mehr dasselbe "es"
die W für einmal Rot ist 0.4865 , die W für zweimal Rot NACHEINANDER ist 0.4865*0.4865
die Wahrscheinlichkeit ist bei JEDEM der einhunderttausend Versuche immer 0.4865
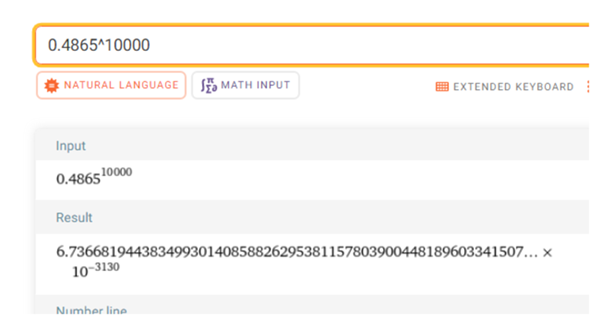
Aber die W für 100000x mal Rot nacheinander ist 0.4865^100000 = so klein, dass der Rechner schlapp macht
Für 10000

die -3130 deutet an , dass es noch 3130 Nullen hinter dem Komma sind , bevor die Ziffern kommen
Ich verstehe bloß nicht, wieso die Wahrscheinlichkeit für mehrere Gewinne hintereinander geringer ist, obwohl bei jedem der einhunderttausend Versuche die Wahrscheinlichkeit immer bei 48,65% liegt.
Also jedes Drehen als einzelnes Ereignis hat immer die Wahrscheinlichkeit 48,65%. Aber das Ereignis, dass 10000 mal hintereinander rot kommt hat eine Wahrscheinlichkeit von (48,65%)^10000. Und damit selbstverständlich deutlich kleiner.
Aber nur, solange i.i.d., oder?