Zustandsvariablen in einem Schaltwerk?
Aufgabe: Bestimmen die Zustandsvariablen und gebe für die Ausgänge c und d die Ausgangsfunktionen an.Hinweis: Wie viele Zustandvariablen benötigt man, um die Ausgangsfunktionen zu beschreiben?
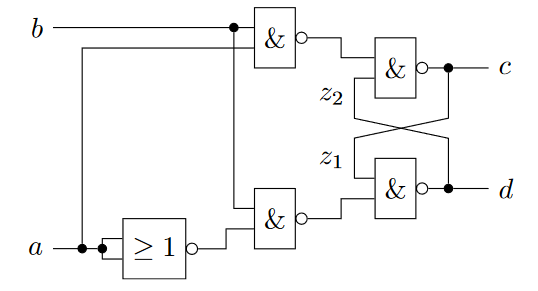
Ansatz: habe mir zunächst überlegt alle Gatter einzeln zu beschreiben und dann zusammenzuführen.
Für z2:
Also ganz unten rechts wäre ja (A NOR A) und dieses dann mit dem NAND-Gatter unten zusammengefügt wäre ((A NOR A)) NAND B). Das fügt man dann mit dem NAND-Gatter ganz rechts zusammen. Das NAND-Gatter auf der einen Seite hat als anderen Eingang (A NAND B) (das ist oben rechts) oder eben die Funktion ((A NOR A) NAND B) und eben wieder (A NAND B). Das käme dann aber zu einer endlos rekurisven Verkettung
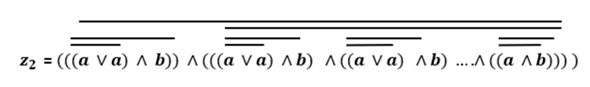
Dann hab ich mir überlegt, dass man ja diese rekursive Verkettung durch z1 und z2 ersetzten kann, also kämen als Funktionen heraus:
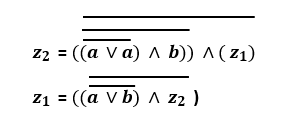
Problem: Ich bin mir nicht sicher, ob das so korrekt ist, oder ob ich das Schaltzwerk nicht doch zu sehr vereinfacht hat. In den nächsten Teilaufgaben sollte man ein Zustandsübergangsdiagramm und eine Zustandstabelle zeichnen, und ich glaube, durch diese Darstellung sind einige Informationen verloren gegangen. Oder passt das soweit?
Und ich verstehe nicht, wie ich die Ausgangsfunktion c und darstellen soll? Klar, c und d sind abhängig von a, b sowie z1 und z2. Aber ist in dem Schaltwerk c nicht das gleiche wie z1? Und d ist doch dasselbe wie z2, oder? Weil z1 wird ja unmittelbar vor c geschaltet und da ja kein Gatter mehr davor ist, ist das doch identisch, oder? Analog bei d und z2.
2 Antworten
Ich empfehle, in einer grösseren Kategorie denken.
Dies vereinfacht die Aufgabe zugleich drastisch!
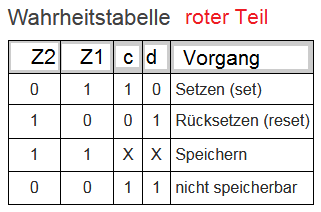
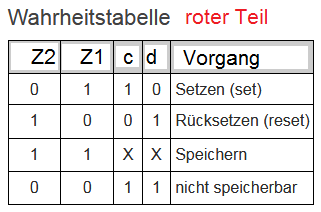
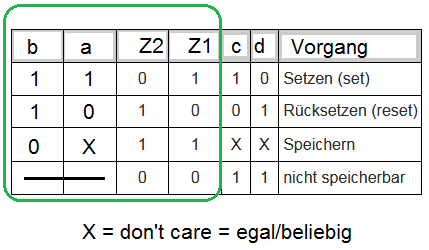
- Zunächst nehme ich mal an, dass die Anschrift ungenau ist. Denn so wie angeschrieben ist tatsächlich Z1=c und Z2=d, was wenig Sinn ergibt.
- Ferner muss man erkennen, dass die Schaltung im rechten, roten Teil keine kombinatorische Schaltung ist, sondern eine sequentielle Schaltung. Ein Flip-Flop, ein sogenanntes NAND-Latch, oder eine Speicherzelle für 1 Bit. Für solche Schaltungen machen Boolsche Gleichungen nur wenig Sinn, da sie rekursiv verkoppelt sind, also nicht eindeutig. Es gibt undefinierte Fälle. Auch Wahrheitstabellen können schon schwierig werden.
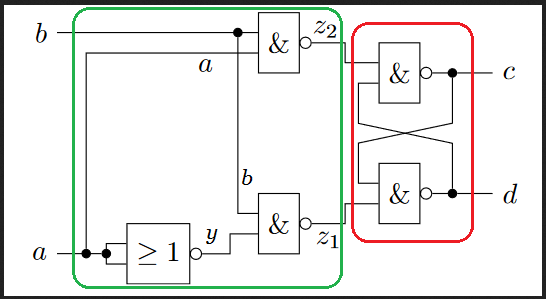
- Du kannst also den grünen und roten Teil separat betrachten:
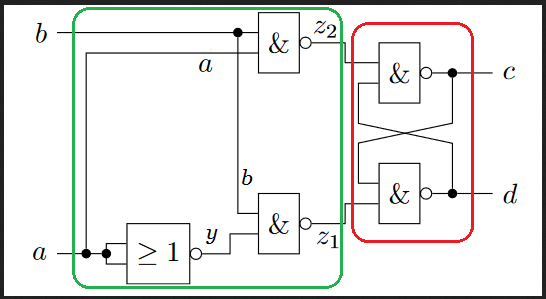
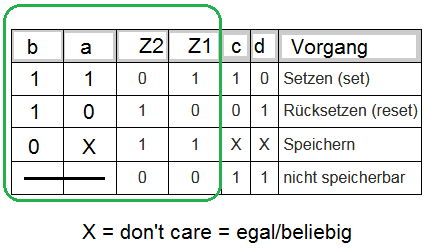
- Vielleicht musst du ja nur die (kombinatorisch) ermittelbaren Variablen Z1 und Z2, so wie ich sie eingetragen habe, in Abhängigkeit von a und b ermitteln.
- C und D ergeben sich dann aus dem Verhalten eines NAND-Latches:
- Wenn man will, kann man noch die Hilfsvariable y einführen, die immer die Negation von a ist.
- Dann muss auffallen, dass Signal b beiden Eingängen zugeführt wird.
- Dies kann sogleich zur Erkenntnis führen, dass bei Z1 und Z2 nur dann etwas ändern kann, wenn b=1 ist (denn ein NAND mit mind. einem Eingang=0 hat am Ausgang immer eine 1).
- Wenn b=1 ist, dann ist Z2= NOT(a), und Z1 = a (weil y die Negation von a ist, und z1 die Negation von y)
- Wenn b=0 ist, kann der Eingang a nichts ausrichten, Z1 und Z2 sind beide = 1. Dies ist der sogenannte Speicherfall beim NAND-Latch, das heisst, der vorherige Zustand von c,d bleibt gespeichert (1,0 oder 0,1)-
- Der grüne Teil der Schaltung stellt also nur sicher, dass der "verbotene" Fall (0,0) zuunterst nie auftreten kann
- Somit kann man mit den Eingängen a,b die Tabelle vervollständigen:
Ich weiß gerade nicht wo dein genau dein Problem liegt, aber lies dich hier ein: