Zahl die durch 7, aber nicht durch 2, 3, 4, 5 oder 6 teilbar ist
6 Antworten
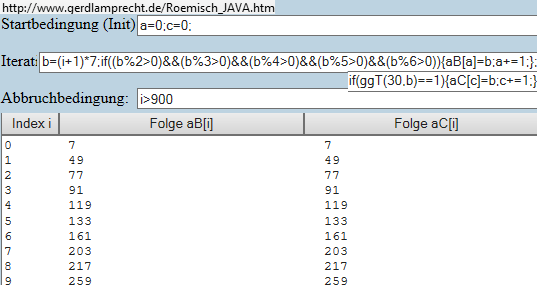
7, 49, 77, 91, 119, ...kurz:
x*7, wobei x teilerfremd zu 2, 3 und 5 sein muss.
Lösung in mathematischer Schreibweise:
f(x)=7*x mit (f(x) mod 2>0)&&(f(x) mod 3>0)&&(f(x) mod 4>0)&&(f(x) mod 5>0)&&(f(x) mod 6>0)
kurz: ggT(30,f(x))==1
weil 30 = 2 * 3 * 5
per Iterationsrechner: http://www.gerdlamprecht.de/Roemisch_JAVA.htm##@Na=0;c=0;@Nb=(i+1)*7;if((b%252%3E0)&&(b%253%3E0)&&(b%254%3E0)&&(b%255%3E0)&&(b%256%3E0)){@Ba]=b;a+=1;};if(ggT(30,b)==1){@Cc]=b;c+=1;}@Ni%3E900@N0@N0@N#
(LINK beinhaltet Code und endet mit N# )
siehe Bild
Mit
http://www.gerdlamprecht.de/Roemisch\_JAVA.htm##@N@B0]=bigc(2,bigc(0,bigc(4,'10','76'),'33'),'7');@N@Bi+1]=bigc(9,@B0],(i+2).toString());@Ni%3E=5@N0@N0@N#
kann man zeigen, dass große Zahlen wie
70000000000000000000000000000000000000000000000000000000000000000000000000231
auch die Bedingung erfüllen.
bigc(9, ist modulo
Der GF - Editor hat hier zwischen Roemisch und _JAVA ein \ hineingefügt, um mich zu ärgern!
...mich auch! Hab schon sämtliche mir bekannte HTML Tricks probiert.
Es muss eine Zahl sein, die ungerade ist - damit fallen schon 2,4, und 6 heraus. Dann darf hinten keine 5 stehen und ihre Quersumme darf nicht durch 3 teilbar sein. Dann musst Du das Einmaleins der 7 durchgehen und kommst auf 7 oder 49.
die kleinste? 7.
die nächste? 7².
Aber alle? das wäre jetzt das einzige, was mich reizen würde.
Alle: Im Intervall von (0,n-1) mit n=7*6*5*4, (3 und 2 entfallen, weil sie Primfaktoren von 6 bzw. 4 sind).
Ab da zyklische Wiederholung.
Evtl. ist die Zykluslänge kleiner (wegen 6=3*2) - aber auf keinen Fall größer.
7 würde gehen ;)
Ne interessante Webseite hast Du da gebastelt.