Wie verwandele ich eine Summe in ein Produkt mithilfe Binomischer Formeln?
Hallo Community,
Ich hätte eine Frage zu einer Aufgabe. Ich habe soweit die binomischen Formeln verstanden und auch teilweise wie man mit binomischen Formeln Summen in ein Produkt umwandelt. Jedoch komme ich bei einer Aufgabe nicht weiter:
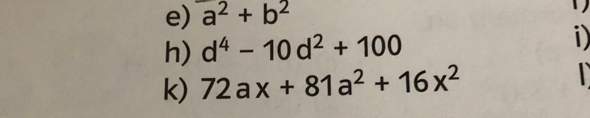
Bei h) komm ich einfach auf keine Lösung. Ich hatte gedacht es wäre vielleicht (d^2-10)^2. Da kommt allerdings d^4-20d+100 raus... Kann mir vielleicht bitte jemand helfen?
5 Antworten
Nicht immer ergeben drei Summanden einen Binom, auch wenn es so aussieht, weil 2 Summanden quadratisch sind. Bei h) hast Du richtig erkannt, dass es d⁴-20d+100 heißen müsste, damit man die quadr. Klammer (d²-10)² bilden kann. Da dies nicht der Fall ist, ist der vorgegebene Term kein Binom!
Ziehst Du aus den Quadraten die Wurzel, und multiplizierst diese Ergebnisse, dann muss der 3. Wert das doppelte davon sein.
Beispiel k: Die Wurzeln aus den Quadraten ergeben 9a und 4x; das Produkt davon ist 36ax. Der 3.Wert lautet 72ax, ist also das Doppelte, somit hast Du hier einen Binom.
e) ist auch kein Binom. Hier fehlt entweder der nicht quadratische dritte Summand, oder aber es müsste Minus statt Plus heißen: werden 2 Quadrate subtrahiert, dann liegt der 3. Binom vor.
Hier soll ja, falls möglich, aus d⁴-10d²+100 ein Produkt gebildet werden, und das ist nicht möglich. Es müsste d⁴-20d²+100 heißen, damit das klappt.
Ja, habe ich auch gerade gesehen und dann gemerkt was Du mir sagen wolltest:)
Das sind die allgemeinen Formeln:
(a + b)^2 = a^2 + 2ab + b^2
(a - b)^2 = a^2 - 2ab + b^2
(a + b)(a - b) = a^2 - b^2
Vielleicht hilft dir das etwas beim Lösen der Aufgaben
Hi,
völlig richtig.
h.) geht nicht wenn es da -10d² steht. bei der binomischen Formel wäre da -20d²
diese h.) geht auch nicht als Produkt von 2 Faktoren zu schreiben da die Gleichung überhaupt keine reellen Lösungen hat.
k.) ist einfach (9a + 4x)²und e.) geht natürlich auch nicht, nicht verwechseln mit a² - b²
LG,
Heni
Du hast nur -10d^2 als mittleren Teil der binomischen Formel. Dazu passt b=5.
Also machst du folgendes.
d^4 -10d^2 +25 +75
(d^2 - 5)^2 +75
bei der Probe hast du einen Fehler gemacht.
d^4 -20 d^2 +100