Wie komme ich von der Normalform zur Scheitelpunktform ohne alle Variabeln zu haben?
Unten im Bild steht die Gleichung. Schreibt mir zu eurer Antwort bitte den Weg auf.
Danke im Vorraus!
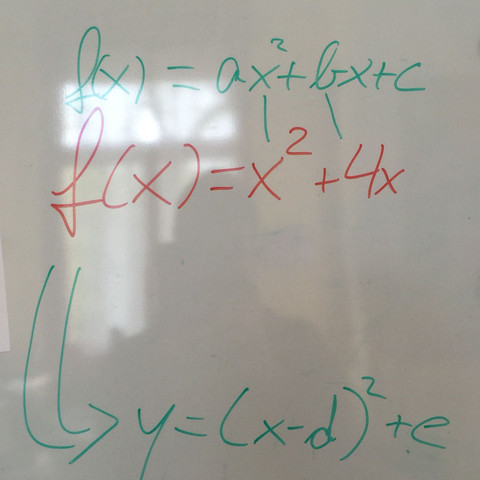
4 Antworten
Allgemeine Form y=f(x)=a2 *x^2+a1 *x +ao
Scheitelkoordinaten x=- (a1)/2 *a2 und y= - (a1)^2/(4 *a2) + ao
scheitelpunktform y=f(x)= a2 *(x +b)^2 + c mit y=c und b= - x
Bei deiner Aufgabe y=a*x^2 +b *x +c ergibt sich
x= - (b)/(2*a) und y= - (b)^2/(4 *a) +c
bei dir werden nur andere Buchstaben verwendet !
HINWEIS : Die Formeln für die Scheitelkoordinaten ergeben sich durch die Umformung der allgemeinen Form mit der "quadratischen Ergänzung" zur Scheitelpunktform"
Du hast 2 Möglichkeiten
1. Du wendest die Formeln für den Scheitelpunkt an
2. Du führst jedes mal neu die "quadratische Ergänzung" durch
MERKE : Die Anwendung von Buchstaben in Formeln ist nicht genormt.Für ein und die selbe Formel,sieht man deshalb,dass verschiedene Buchstaben verwendet werden !!!
Buchstaben bei dir y=f(x)= a *x^2 + b *x +c
Meine verwendeten Buchstaben waren
y=f(x)=a2 * x^2 + a1*x + ao
also ist a=a2 und b=a1 und c=ao
TIPP : Rechne ein paar Proberechnungen mit werten durch und kontrolliere so die Formeln.Dann entscheide,welche Buchstaben du in den Formeln verwenden willst.
Das ist doch so einfach... binomische Formel
x²+4x+2² - 2²
= (x+2)² - 4
S(-2 ; -4)
Durch quadratische Ergänzung
z.B x^2 + 8x + 15
(x^2 + 8x + 4) -4+ 15
(x +4)^2 + 11
-b/ 2a kann ich ja schlecht anwenden (oder kann ich davon ausgehen das a=1 ?