Normalform in Scheitelpunktform berechnen?
Hallo,
gegeben ist die Normalform f(x) die ich in eine Scheitelpunktform umwandeln soll. Bei einem Schritt wusste ich nicht mehr weiter könnt ihr mit erklären wie es weiter geht?
Danke
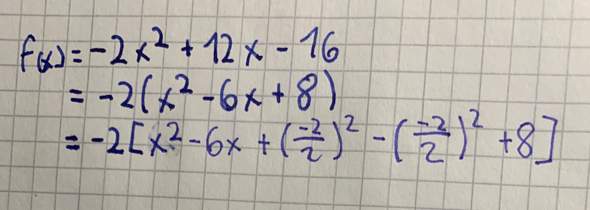
4 Antworten
Du hast mit (-2/2)² ergänzt, aber eigentlich brauchst du hier (-6/2)². Siehst du, warum das so ist?
-2 Ausklammern ?sehr gut , Richtig !
-2 * ( x² - 6x + 8 )
qua ergänzung , aber richtig bitte :))
mit (-6/2 ) = -3 findet man sie
-2 * [ (x - 3)² -9 !!! + 8 ]
-9 , weil man +9 zuviel dazugetan hat
-2 * [ (x-3)² - 1 ]
-2*(x-3)² + 2
ScheiPu ( +3 / + 2 )
Quadratische Ergänzung, bääh.
Wenn du dir die Lösungsformeln anschaust, dann wirst du nach wenig Arbeit darauf kommen, das
die x-Koordinate des Scheitelpunktes ist, das musst du dann nur noch als x einsetzen, dann hast du die y-Koordinate des Scheitelpunktes.
xs= 3
ys= 2
f(x) = -2(x - 3)² + 2
fertig.
Dein ,,a" ist -2, das setzt du einfach ein.
Du musst nichts weiter machen, als das stur anwenden, dann kriegst du immer den Scheitelpunkt, das funktioniert perfekt bei quadratischen Funktionen.
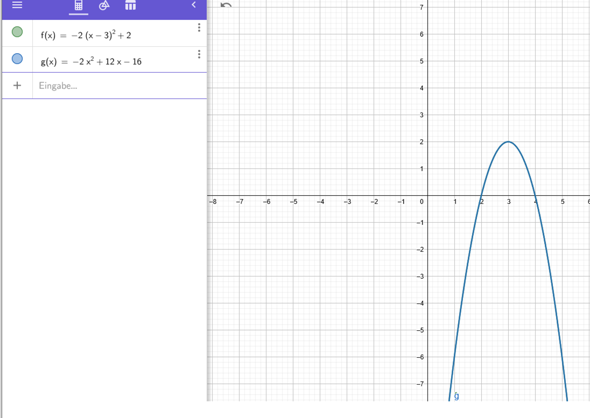
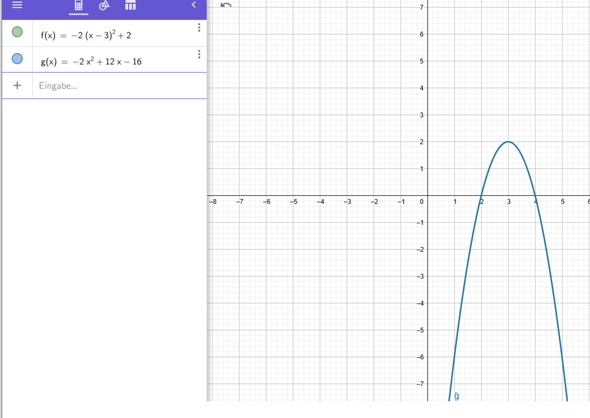
Ich bekomme am Ende -2(x + 3)² + 2 nicht -2(x - 3)² + 2 was hab ich falsch gemacht?
Obacht, vergess das Minus nicht.
Wie du bei GeoGebra selbst ziehst, ist deine Parabel nach rechts verschoben, da steht immer ein Minus in der Scheitelpunktform, also -3
Das -6x stammt aus der binomischen Formel 2ab. a = 1 (wegen x^2), also muss b = -3 sein. dementsprechend muss mit +(-3)^2 - (-3)^2 ergänzt werden.
So geht es dann weiter:


Ich bekomme am Ende -2(x + 3)² + 2 nicht -2(x - 3)² + 2 was hab ich falsch gemacht?