Wie kann man den Funktionsterm ermitteln?
Wie kann ich den Funktionsterm ermitteln nur mit Hilfe des Graphen.
Danke im Voraus!
5 Antworten
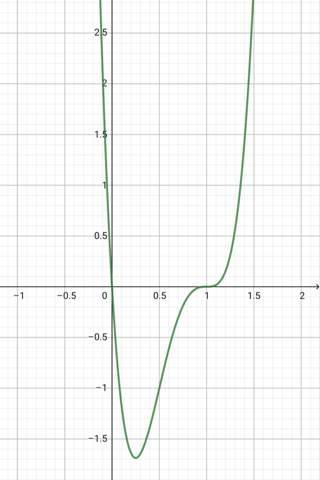
Bei der Nullstelle 1 sieht es aus wie x^3
also
(x-1)^3
Wenn du jetzt ein x heranmultiplizierst kriegst du die Nullstelle bei 0 unter.
x(x-1)^3
Jetzt noch einen passenden Koeffizienten finden.
Man sieht bei x=0.5 ist y=-1
Also
-1=a•0.5•(-0.5)^3
1=a•0.5^4
a=16
Die Funktionsgleichung wird wohl lauten:
f(x)=16•x•(x-1)^3
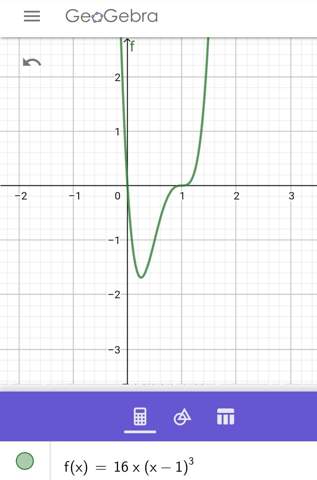
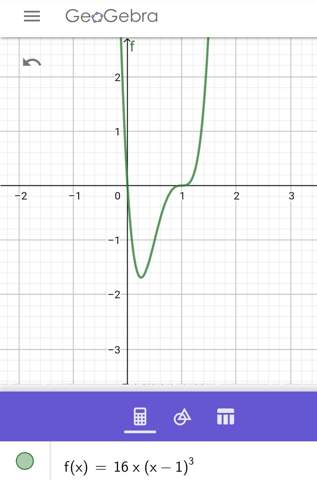
x^5 sieht am Sattelpunkt (der Nullstelle) etwas anders aus. Wenn du dich oft genug mit Kurvendiskussion beschäftigst kriegst du einen Blick dafür.
Man sollte immer mit dem niedrigsten Grad der Polynomfunktion anfangen und erst wenn das nicht passt, die Gleichung erweitern.
Über die Funktion ist folgendes bekannt:
- es existieren zwei Nullen
- es existiert ein offensichtliches Minimum
- für die zweite Nullstelle gilt, dass diese ebenfalls eine Steigung von 0 hat (was bedeutet das?)
- bei der 2. Nst ist noch eine andere Besonderheit ;)
- eine Wendepunkt ist auch gut erkennbar
Anhand der Informationen kannst Du feststellen, welchen Grad die Funktion mindestens haben muss
Eine Fkt. des n. Grades hat maximal n Nullstellen. Nun könnte man argumentieren "Zwei Nullstellen, also Fkt. des 2. Grades". ist aber falsch. Hier kommen die Extra ins spiel.
Überleg mal, wie viele Extrema eine Funktion des n. Grades maximal haben könnte. Mit diesen Infos plus den Nst. kannst kannst Du die "Rohformel" aufstellen.
Werte einsetzen, Gleichungssystem lösen, fertig!
Nur, was das mit Chemie zu tun hat, weiß ich nicht!
kommt drauf an ob es sich um ein Polynom handelt oder nicht (oder politisch korrekter um eine ganzrationale Funktion),
Da kannst du dann die verschiedenen bedingungen für Sattelpunkte, Wendepunkte, Extrempunkte aufschreiben bzw. ablesen vom Graph.
Und mal beginnend, bei n=3 die Polynome n-ten grades durchprobieren ob eins passen könnte.
Will sagen, du nimmst an, dass es ein Polynom 3-ten grades ist und versuchst mit den Bedingungen die koeffizienten in ax^3+bx^2+cx+d zu bestimmen.
klappts nicht, verwirfst du das und gehst zu eine grad 4 polynom über und testest dort.
Irgendwann wirst du hoffentlich fündig :-)
bleibt nur zu hoffen dass es sich nciht um eine gebrochenrationale Funktion (oder gar was ganz Anderes) handelt.
Aber da kein Definitionslücken oder so offensichtlich erkennbar sind, gehe ich da mal nicht davon aus.
zu dem was man ablesen kann:
Nullstellen bei (0,0) und (1,0).
Minimum bei (0,25; -1,7)
Wendepunkt ungefähr bei (0,575; -0,7) (bringt dir eher bei der nahcträglichen Kontrolle was)
Sattelpunkt offensichtlich bei (1;0) (ist die Nullstelle von oben)
Ansosnten kannst du da so viele Punkte des Graphen ablesen wie es dr beliebt.
Ich würde mich aber makl einfach auf die Nullstellen, das Minimum und den Sattelpunkt und die damit verbundenen Punkte beschränken :-)
Du nimmst die allgemeine Form
f(x) = y = ax^4 + bx^3 + cx^2 + dx + e und setzt von 5 verschiedenen Punkten die x- und y-Koordinaten ein. Du kannst auch y=0 in die 1. Ableitungen an Estremstellen und in die 2. Ableitung an Wendestellen einsetzen. Dann erhältst du ein Gleichungssystem, dass du lösen kannst.
Dadurch, dass Du einen Wert x abliest und den dazugehörigen y-Wert. Aus beiden kann man die Funktion dann berechnen.
Die kubische Funktion ist um 1 nach rechts verschoben. also hast du schon mal eine plus eins als konstante drin.
oh: ich sehe gerade das sie nur teilweise kubisch ist.
Wenn du gut drauf bist, kannst du den Spaß noch ausmultiplizieren.