Wie kann ich bei dieser Aufgabe die länge der Seile herausfinden?
Hallo, wäre nett wenn ihr mir bei dieser Aufgabe helfen könntet wie man auf die länge der Seile kommt...
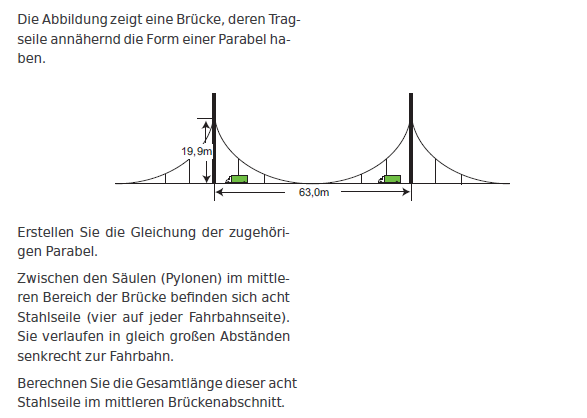
Aufgabe: siehe Bild
Danke
5 Antworten

Der Scheitelpunkt, also (0|0), der Parabel liegt 31,5 m von den beiden Pylonen entfernt. Du hast außerdem die Punkte (-31,5|19,9) und (31,5|19,9). Damit erechnest du die Parabel.
Die Seile sind so gespannt, dasss sie die Strecke von 0 bis 31,5 in drei gleiche Teile teilen, also ist jeder Teil 10,5 m breit. Entsprechend musst du den y-Wert für 10,5 und 21 berechnen. Für die Gesamtlänge nimmst du die y-Werte jeweils mal 4 (du hast 4 kürzere und 4 längere Seile), zählst die Ergebnisse zusammen, und fertig!

Falls du die Parabel schon hast, einfach so sehen. Du hast den Punkt auf der x und der y achse. Und du weißt, dass vier seile auf einer seite sind. Und du kennst due hälfte von 63, also die länge der parabel auf der einen seite. Diese Teilst du durch vier und du hast die x koordinate. Dann setzt du das in die Parabel funktion ein und du erhälst du y koordinate, was dann deine höhe ist.
Das machst du dann 2 mal so weiter, indem du einfach deinen x wert mal 2 und mal 3 nimmst und immer wieder einsetzt.
Da es achsensymmetrisch ist, musst dudn as auch nur für die eine seite machen ^^
hoffe ich konnte helfen :)

y Wert = 19,9 m
x wert = 31,5 m
Parablgleichung Errgebnisder Seillänge: 8 Seil längen x 2 Brücken

Hallo,
relevant für die Lösung der Aufgabe ist nur der mittlere Bereich der Brücke (der zwischen den Pylonen). Wenn Du die Parabel, die das Tragseil beschreibt, so in ein Koordinatensystem einzeichnest, daß der tiefste Teil den Koordinatenursprung berührt und die beiden Pylonen bei x=-31,5 und x=31,5 stehen, hast Du drei Punkte, mit denen Du die Funktionsgleichung bestimmen kannst: (-31,5|19,9), (0|0) und (31,5|19,9).
Die allgemeine Form einer Parabel lautet ax²+bx+c, wobei c den Schnittpunkt mit der y-Achse bezeichnet, der hier gleich Null ist.
Also: f(x)=ax²+bx.
Wenn Du die beiden gegebenen Punkte in diese Gleichung einsetzt, bekommst Du ein Gleichungssystem, mit dessen Hilfe Du a und b berechnen kannst:
(-31,5)²a-31,5b=19,9
31,5²a+31,5b=19,9
Dies liefert für a die Lösung 398/19845 und für b die Lösung 0.
Somit lautet die Gleichung der Parabel f(x)=x²*398/19845
Um die Länge eines der senkrechten Seile zu ermitteln, machst Du Dir die Tatsache zunutze, daß sie im gleichen Abstand voneinander aufgehängt sind, also alle 10,5 m. Du mußt also für x die Werte 10,5 und 21 einsetzen. Der dazugehörige Funktionswert entspricht der Länge eines Seiles. Wegen der Symmetrie reicht es, die Werte dieser beiden zu addieren und die Summe
mit 4 zu multiplizieren.
Herzliche Grüße,
Willy

Wenn eine Parabel den Scheitelpunkt (0|0) hat, kannst Du es Dir auch noch einfacher machen, denn dann hat sie die allgemeine Form f(x)=ax². Du brauchst also nur noch einen Punkt außer (0|0) einzusetzen, um a zu berechnen.
In Deinem Fall wäre 31,5²*a=19,9, also a=19,9/31,5²=398/19845.
Gruß, Willy

Wenn du die Parabel so legst, dass der Scheitelpunkt auf der Koordinate (0;0) liegt, dann ist ein weiterer Punkt bei (31,5;19,9). Das reicht um die Parabel eindeutig zu bestimmen. Danach überlegst du dir die X-Koordinate der 2 Seile rechts von (0;0) und berechnest ihre Y-Koordinate (=Seillänge). Jede Seillänge kommt vier mal vor.
Den Rest musst du selbst machen ;-)