Wie dieses Integral weiter lösen?

Hi ich brauche Hilfe bei diesem Integral. Wie mache ich hier weiter?

Answer 1

[ChrisGE1267]

Sobald von einem parameter-abhängigen bestimmten Integral die Rede ist, wird es wohl auf Feynman‘s Trick hinauslaufen (Differentiation unter dem Integral)…

Woher ich das weiß: Studium / Ausbildung – Dr. rer. nat. Analytische & Algebraische Zahlentheorie

Answer 2

[mihisu]

Ich glaube nicht, dass du so weiterkommen wirst. Sowei ich das sehe, wird es keine elementare Stammfunktion geben.

https://de.wikipedia.org/wiki/Elementare_Funktion

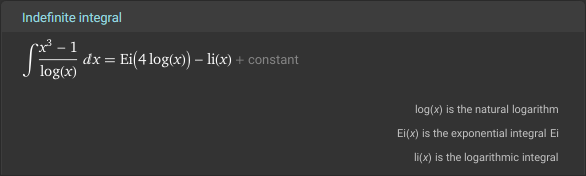
Wenn ich das unbestimmte Integral beispielsweise WolframAlpha weitergebe, erhalte ich...

[https://www.wolframalpha.com/input?i=Integrate%5B%28x%5E3+-+1%29%2FLog%5Bx%5D%2C+x%5D]

... mit den nicht-elementaren Funktionen Ei (Integralexponentialfunktion) und li (Integrallogarithmus).

============

Wie kommt man hier dennoch zu einem Ergebnis? ... Du brauchst gar nicht die Stammfunktion bzw. das unbestimmte Intregal zu berechnen. Du hast ein bestimmtes Integral mit konkrete Integralgrenzen 0 und 1 gegeben.

Zunächst einmal ist auch im Hinweis ein x^λ mit allgemeinerem λ zu finden, wobei neben λ = 3 auch λ = 0 interessant sein soll.

Als meinen konkreteren Hinweis möchte ich nun hinzugeben...

Betrachte eine Funktion f, welche durch

$f(\lambda):=\int\limits_{0}^{1}\frac{x^\lambda - 1}{\ln(x)}\,\text{d}x$

gegeben ist.

Nutze nun die gleiche Substitution, wie bei dir in deinem Lösungsversuch, um

$f(\lambda)=\int\limits_{-\infty}^{0}\frac{\text{e}^{\lambda\cdot u} - 1}{u}\cdot \text{e}^{u}\,\text{d}u$

zu erhalten.

Stelle nun fest, dass einerseits f(3) der gesuchte Wert ist und andererseits

$f(\lambda)=f(0)+\int\limits_{0}^{\lambda}f'(\tilde{\lambda})\,\text{d}\tilde{\lambda}$

ist. Denn wenn du f′(λ) betrachtest, wirst du feststellen, dass du das in f′(λ) vorkommende Integral leichter lösen kannst. Und auch das Integral über f′(λ) sich recht einfach berechnen lässt.

====== Ergänzung: Lösungsvorschlag zum Vergleich ======

Comments

[fires609ae]

Vielen Dank du hast mir echt den Arsch gerettet, darauf wäre ich selber niemals gekommen.

Answer 3

[PWolff]

Die Integrale, die du zuletzt da stehen hast, führen auf die Integralexponentialfunktion, die sich nicht elementar darstellen lässt.

Vielleicht führen ähnliche Funktionen weiter (mit etwas abgewandelter Substitution): https://de.wikipedia.org/wiki/Integralexponentialfunktion#Abgewandelte_Integralexponentialfunktionen

Answer 4

[snowie535]

Ich würde es mit partieller Integration versuchen