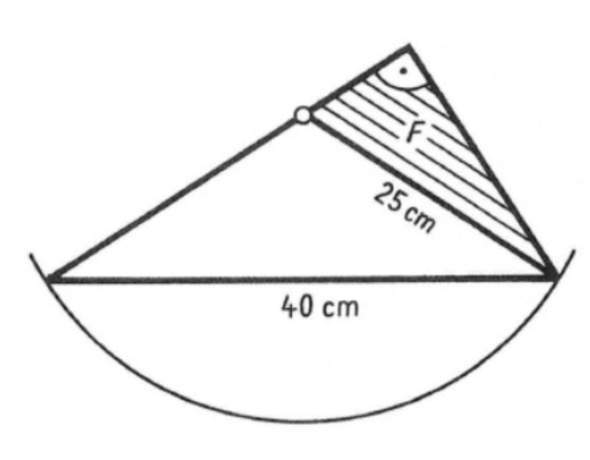
Wie berechnet man die schraffierte Fläche?
3 Antworten
Berechnung
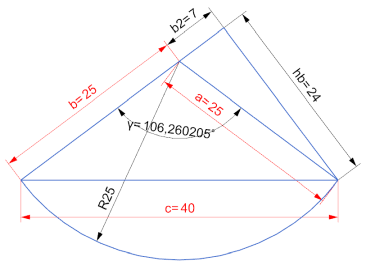
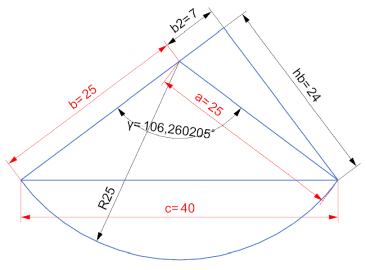
γ = (180 - (ARCCOS((a^2 - b^2 - c^2) / (-2 * b * c)) /PI()*180) - ARCCOS((a^2 - b^2 - c^2) / (-2 * b * c)))
γ = (180 - (ARCCOS((25^2 - 25^2 - 40^2) / (-2 * 25 * 40)) /PI()*180) - ARCCOS((25^2 - 25^2 - 40^2) / (-2 * 25 * 40)))
γ = 106,260205°
---
hb = a * SIN(γ)
hb = 25 * SIN(106,260205)
hb = 24 cm
---
b2 =Wurzel(a² - hb²)
b2 =Wurzel(25^2 - 24^2)
b2 = 7 cm
---
F = hb * b2 / 2
F = 24 * 7 / 2
F = 84 cm²
Hallo,
Du kannst auch einfach den Pythagoras benutzen. Nenne die kürzere Kathete des schraffierten Dreiecks x und die längere y.
Dann gilt:
(25+x)²+y²=40²;
außerdem gilt:
x²+y²=25².
Beide Gleichungen nach y² auflösen und die jeweiligen rechten Seiten der so umgeformten Gleichungen gleichsetzen. x² hebt sich dann auf beiden Seiten auf, so daß für x eine lineare Gleichung übrigbleibt.
Zur Kontrolle: x=7, y=24, Fläche=7*24/2=84 Flächeneinheiten.
Herzliche Grüße,
Willy
Es fehlt die Angabe, ob der gekennzeichnete Punkt der Mittelpunkt des Kreises ist.
Falls es so ist, handelt es sich bei dem unteren Dreieck um ein gleichschenkliges Dreieck, von dem 3 Seiten bekannt sind. Der Mittelpunktswinkel kann mittels Sinus oder Kosinussatz berechnet werden.
Damit können auch die Winkel und Seiten der gesuchten Fläche sowie die Fläche selbst bestimmt werden.
Mittelpunktswinkel im unteren Dreieck.
sin(γ / 2) = (40 / 2) / 25
γ = 106,26°
Die Ergänzung zu 180° ergibt den linken Basiswinkel des schraffierten Dreiecks:
180° - 106,26° = 73,74°
Mit diesem Winkel und der Basis von 25 cm lassen sich die beiden Katheten des schraffierten Dreiecks berechnen:
b = 25 * cos(73,74°) = 7,00
a = 25 * sin(73,74°) = 24,00
Fläche A:
A = (1 / 2) * 7 * 24 = 84 cm²
Es ist der Mittelpunkt de s Kreises kannst du mir den Schritt mit Cosinus und Sinus erklären?