Wie berechne ich, wie viel Kubikmeter Erde bereitgestellt werden muss?
Aufgabe: Entlang eines 800m langen Kanals soll ein Schutzwall aufgeschüttet werden. Dieser hat einen parabelförmigen Querschnitt (Breite: 6m; Höhe 2m)
als Funktion habe ich: f(x) = -2/9x² + 2
b) Berechne, wie viel Kubikmeter Erde bereitgestellt werden müssen.
5 Antworten
Der Schutzwall ist ein Prisma. Die Fläche zwischen Parabel und x-Achse ist die Grundfläche. Die musst du noch berechnen.
Und die Höhe sind 800 m.
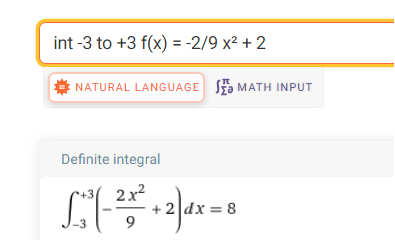
8 m² Querschnittsfläche
800 m lang
Gebraucht werden 8 * 800 = 6400 m³
.
..
...
hierher scheinen deine 12 zu kommen ( 2 mal 3 mal 2 )
Rechnest du 12 - 8 , erhältst du die grünPunkt-Fläche
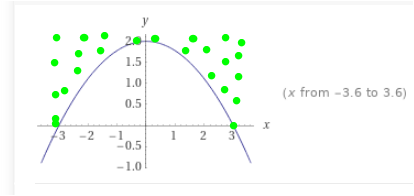
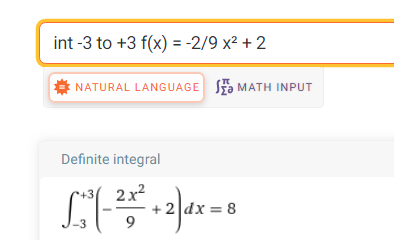
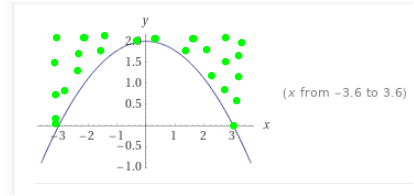
Du brauchst die Fläche unter der Parabel. Dafür musst du das Integral berechnen.
Also ich habe für das Integral = 8 raus und für die Fläche = 12
Dann subtrahiere ich beides also: 12 - 8 = 4
und die 4m² * 800m = 3200m^3?
Mir ist unverständlich, was die Fläche ist, wenn das Intergral 8 ist. Worin unterscheiden die beiden sich?
UND Warum subtrahierst du sie? Welcher Gedanke steht dahinter?
Einfach weil subtrahieren schöner ist als addieren oder multiplizieren? Du könntest sie auch dividieren....
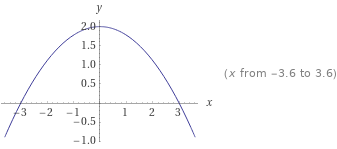
Die Fläche unter dem Graphen über der x-Achse ist 8 (m²).
https://www.wolframalpha.com/input/?i=%3D+-2%2F9x%C2%B2+%2B+2
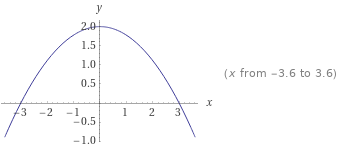
Integral berechnen
Also ich habe für das Integral = 8 raus und für die Fläche = 12
Dann subtrahiere ich beides also: 12 - 8 = 4
und die 4m² * 800m = 3200m^3?
Stimmt das?