Was ist eine Asymptote?
ist eine Asymptote eine Kurve oder eine Gerade , an die sich der Graph einer Funktion immer mehr annähert Ohne die zu schneiden
4 Antworten
Erst im Unendlichen ist die immer weitere Annäherung für eine Asymptote gefordert davor kann der Graf die Asymptote (Kurve oder Gerade) einmal oder mehrmals schneiden
Wenn man es genau nimmt ist eine Asymptote an eine Funktion f für x gegen unendlich eine Funktion g für die gilt:
Das "nicht Schneiden" ist also nicht notwendig Voraussetzung für das Vorliegen einer Asymptote.
Für x gegen unendlich gibt es keine vertikale Asymptote. Der Beweis sowie die Beschreibung von vertikalen Asymptoten als Grenzwert werden dem Leser/der Leserin zur Übung überlassen.
Kochrezepte habe ich (noch) keine gefunden, aber ich muß zugeben dass ich bisher nicht in der Lage war eines der Bücher von Anfang bis Ende zu lesen. Aber ich will nicht verhelen dass ich die Bücher von Heuser als Schätze der Analysis und Funktionalanalysis betrachte und sie auch so behandle :-).
Vorweg : A können auch Kurven sein , es muss keine Gerade sein!
.
Nicht falsch , was du schreibst . Aber gleich ein Beispiel zur Klarstellung

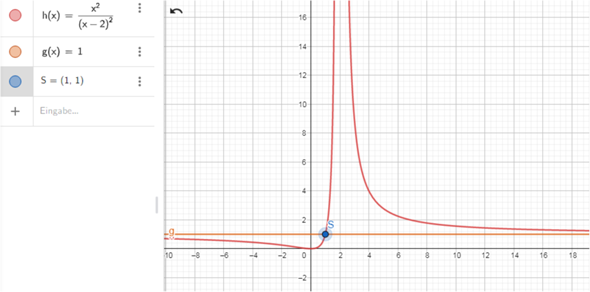
so sieht der Graph aus
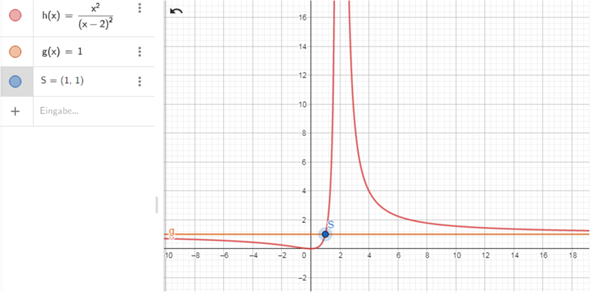
die A f(x) = 1 ist A für den rechten roten Ast , auch für den linken , schneidet aber trotzdem.
"Richtig" A ist sie erst im Unendlichen
.
Aber Abstand zwischen A und Graph geht gegen Null , wird es aber nicht , denn das wäre ein Schnittpunkt .
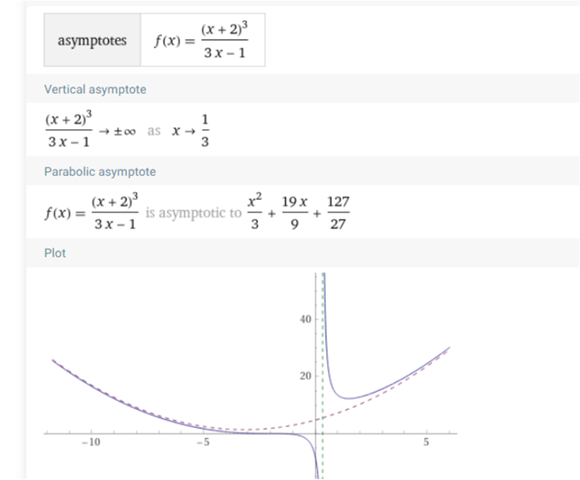
und noch einen hinterher : wegen des Vorweg
hier
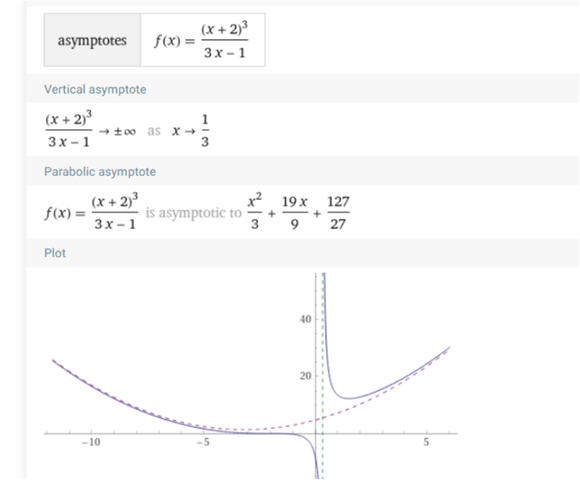
ist eine Parabel die A für beide Kurvenäste
.
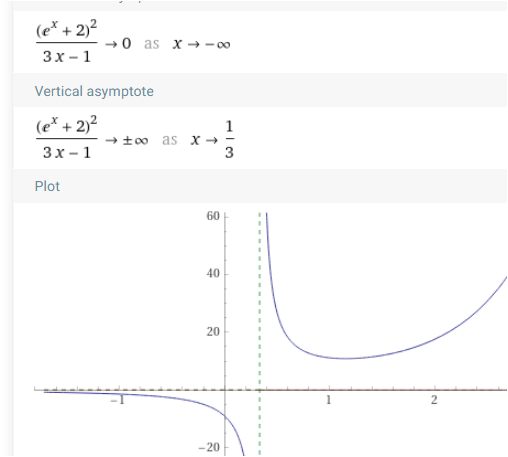
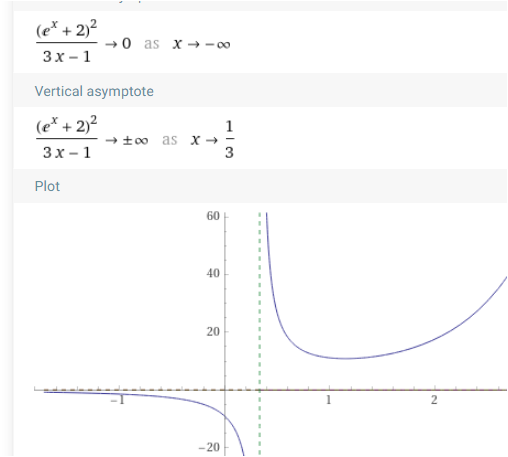
und als letztes . . ::Es gibt auch A , die nur A für eine Seite der Kurve sind Hier .
nur links ist f(x) = 0 A
.
Graphiken oben zitiert von hier

Nicht ganz, das mit der Annäherung stimmt, aber die
Funktion kann die Asymptote beliebig oft schneiden.
Außer für vertikale Asymptoten ;)