Was ist die Umkehrfunktion von Polynomen nten Grades?
Hey Leute!
Ich weiß, ist schon spät, aber ich habe dennoch eine Frage an Euch:
Gibt es eine Formel, mit de man allgemein die Umkehrfunktion eines Polynomes von ntem Grad bestimmen kann? Also bei n = 1 hat man ja (x-b)/a = y(x) als Umkehrfunktion Bei n " 2 ist (-b +/-sqrt(4ax + bx - 4ac))/(2a) die Umkehrfunktion.
Nur wie kann man das Spielchen auf alle n Element N übertragen?
Danke schon mal für Eure Antworten, und pennt gut!
JTR
4 Antworten
Hi,
ein Polynom y n-ten Grades ist allgemein eine Funktion der Form:
y = Sn m=0 am*xm; an <> 0 ; am e R
Um nun die (sofern über dem gesuchten Intervall vorhandene) Umkehrfunktion zu finden, muss man eine Darstellung f(y) finden.
Also muss man nach x auflösen.
Bsp:
f(x) = y = 2x+1
-> x = (y-1)/2
-> f^-1(x) = (x-1)/2
Ich hoffe ich hab keinen Fehler eingebaut.
Das Auflösen nach x ist im Allgemeinen allerdings nicht möglich, da Gleichungen bis einschließlich vierten Grades in Radikalen allgemein auflösbar sind.
Ich hoffe Du meintest das so wie ich es verstanden habe ;)
Gruß Turtok
Wie Turtok schreibt: Wenn Du eine grF n-ten Grades umkehren willst, musst Du eine Gleichung n-ten Grades lösen. Es gibt zwar für die Gleichung 3. Grades noch (Cardanische) Formeln, aber dann hilft i.A. nur noch eine Näherungsrechnung.
Nein, das geht nicht allgemein. Damit es eine Umkehrfunktion gibt, muss die Funktion bijektiv sein. Das bedeutet zu jedem f(x) darf es nur genau ein x geben. Es gibt natürlich solche Polynome die bijektiv sind.
Ansonsten musst du den Wertebereich einschränken. Dann hast du eine Teilweise Umkehrfunktion.
Außerdem ist Problem ist mit den Nullstellen von Polynomen verbunden. Da es nach dem 4. Grad keine allgemeine Lösungsformel für die Nullstellen gibt, gibt es auch keine für die Umkehrfunktion (selbst wenn eine existiert).
Dann ist das nur noch in Spezialfällen analytisch machbar z.B. wenn du die Funktion als eine Verschiebung in y und x von x^n schreiben kannst. Also die Form f(x)=(x+a)^n+b
Grüße Cooky
Edit:
Die allgemeine Form (zeigt es in der vorherigen Antwort nicht richtig an):
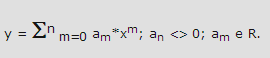
Wie es im allgemeinen aussieht, ist mir klar!
Nur will ich wissen, wie man das umformen kann! :D
Das schrieb ich bereits in der ersten Antwort.
"Um nun die (sofern über dem gesuchten Intervall vorhandene) Umkehrfunktion zu finden, muss man eine Darstellung f(y) finden. Also muss man nach x auflösen."
Mit anderen Worten: Man findet die Umkehrfunktion, in dem man y(x) nach x= auflöst.
Ja? Nur wieso ist das so, dass bei n > 4 keine Invertierungen mehr möglich sind?