Warum ist das Skalarprodukt gleich Null, wenn die Vektoren senkrecht aufeinander stehen (orthogonal)?
Kann mir jemand erklären, weshalb das so ist? Vielen Dank :)
6 Antworten
Warum ist das Skalarprodukt gleich Null, wenn die Vektoren senkrecht aufeinander stehen (orthogonal)?
Das ist äquivalent, gleichbedeutend.
Da trifft sozusagen das abstrakt-Mathematische mit dem anschaulich-Geometrischen zusammen, auch in der Physik, wo beispielsweise die Arbeit bei einer Verschiebung um den Vektor |Δr› mit konstanter Kraft |F› durch
(1.1) ΔW = ‹F|Δr› = ‹Δr|F›
(das Skalarprodukt ist symmetrisch, respektive hermitesch, wenn es um Komplexe Vektorräume geht) gegeben ist und bei Drehungen des Koordinatensystems gleich bleibt.
Skalarprodukt und Betrag, Skalarprodukt und WinkelMan kann bei (1.1) noch ein
(1.2) … = ||F›|·||Δr›|·cos(∠(|F›, |Δr›))
= √{‹F|F›·‹Δr|Δr›}·cos(∠(|F›, |Δr›))
hinzufügen.
Über das Skalarprodukt lassen sich sowohl die Beträge von Vektoren als auch der Cosinus des Winkels und damit der Winkel zwischen zwei Vektoren definieren.
Es ist eigentlich Jacke wie Hose, welches durch welches definiert wurde:
Vom geometrischen Standpunkt her kann sagen, das Skalarprodukt zweier ℝ²-Vektoren (ℝ² ggf. als 2D-Unterraum, also als Ebene des ℝⁿ) so definiert ist, dass es dann gleich Null ist, wenn auch anschaulich der Winkel zwischen ihnen 90° bzw. ½π beträgt. Dies lässt sich dann abstrahieren und somit verallgemeinern.
Vom abstrakten Standpunkt her kann man sagen, das Skalarprodukt sei (in einem reellen Vektorraum) einfach ganz abstrakt als Abbildung V→ℝ mit bestimmten Eigenschaften, Orthogonalität sei einfach dadurch definiert, dass das Skalarprodukt gleich Null ist. Das lässt sich auf die anschauliche Geometrie anwenden.
Vektorprodukt und QuaternionenEine Art Gegenstück des Skalarprodukts ist das Vektorprodukt, das genau dann 0 wird, wenn das Skalarprodukt maximal ist und umgekehrt.
…könntest du mir eventuell noch erklären, weshalb das Vektorprodukt…, … wenn die Vektoren aufeinander liegen, gleich 0 ist, …?
Auch hier könnte man abstrakt sagen, es sei einfach so definiert. Vor allem aber ist das Kreuzprodukt sozusagen nur „zufällig“ in 3D ein „Vektorprodukt“. Eigentlich müsste man es als antisymmetrischen Tensor (2. Stufe, also Matrix) auffassen, aber die hat in 3D eben 3 unabhängige Komponenten und kann mit einem Vektor identifiziert werden.
Auch das Vektorprodukt lässt sich auf anschaulich-Geometrisches anwenden und anschaulich-geometrisch deuten, auch physikalisch. So ist das Drehmoment
(2) |M› = |r›×|F›,
einer am Ort |r› von einem Drehpunkt aus angreifenden |F› die Kraft ein Kreuzprodukt, und die Maßeinheit ist dieselbe wie bei der Arbeit, obwohl das was völlig anderes ist.
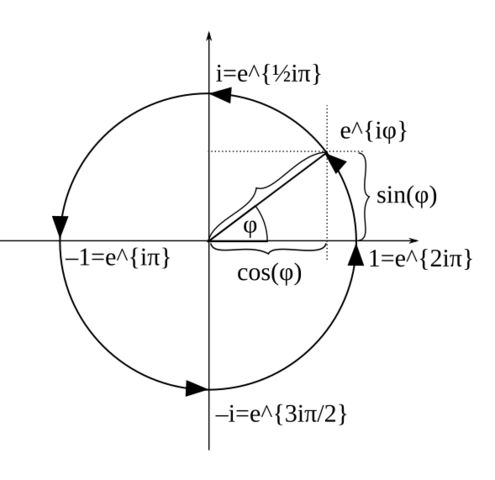
Komplexe Zahlen und Quaternionen Ich weiß nicht, wie weit Du mit den Komplexen Zahlen vertraut bist. Sie lassen sich als Ebene mit zwei Achsen darstellen, den Reellen Zahlen und den Imaginären Zahlen, den reellzahligen Vielfachen der Zahl i, die durch
(3.1) i² = –1
definiert ist. Eine Komplexe Zahl lässt sich durch
(3.2) z = x + i·y, x,y, reell
darstellen, aber nach der Euler'schen Formel
(3.3) e^{iφ} = cos(φ) + i·sin(φ)
auch als
(3.4) z = r·e^{iφ},
wobei φ ein Winkel ist, den eine Komplexe Zahl (als Pfeil darstellbar) mit der positiven Reellen Achse bildet (s. Schaubild).
Die Komplexen Zahlen haben den Vorzug, dass man alle Rechenarten fast uneingeschränkt dort anwenden kann (durch 0 dividieren geht freilich auch da nicht).
Sie sind also eigentlich „saturiert“. Dennoch lassen auch sie sich erweitern.
Inpiriert durch die Komplexen Zahlen fragte der Sohn des irischen Mathematikers William Hamilton seinen Vater einmal, ob er auch Zahlentripel (also Vektoren) miteinander multiplizieren könne, und dieser suchte eine - umkehrbare - Multiplikation und fand keine.
An ihrer Stelle fand er die Quaternionen, bei denen es außer der 1 noch i, j und k gibt, sodass
(4.0) i² = j² = k² = –1
und
(4.1) i·j = –j·i = k
(4.2) j·k = –k·j = i
(4.3) k·i = –i·k = j
ist. Eine sogenannte reine Quaternion ist eine Quaternion, deren reelle Komponente gleich 0 ist. Das Produkt zweier reiner Quaternionen hat eine reelle Komponente, die dem Negativen des Skalarproduktes entspricht; die Vektorkomponenten sind gleich dem Vektorprodukt der beiden Vektoren:
q₁ = (0 ¦ |v₁›)q₂ = (0 ¦ |v₂›)
q₁q₂ = (–‹v₁|v₂› ¦ |v₁›×|v₂›).
Wie bei Komplexen Zahlen multiplizieren sich auch bei Quaternionen die Beträge.
Das Skalarprodukt hängt direkt mit dem eingeschlossen Winkel zusammen:
a*b = |a|*|b|*cos((a,b))
Wenn der Winkel nun 90° beträgt, dann stehen die Vektoren senkrecht aufeinander. Der cos(90) ist 0.
Daraus folgt, dass das Skalarprodukt 0 sein muss, wenn die zwei Vektoren einen Winkel von 90° einschließen:
a*b = |a|*|b|*0 a*b = 0
Wow ich danke euch, hab den Sinn nun endlich verstanden
0° und 180°. Bei 270° würden sie wieder orthogonal sein.
Skalarprodukt ist dann nicht 0, sondern Maximal.
Der cos(0) bzw der cos(180) ist 1; somit ist das Skalarprodukt maximal und entspricht nur noch dem Produkt der Längen:
a*b = |a|*|b|*1
Hierbei kommen jetzt natürlich immer unterschiedliche Ergebnisse, je nach Längen heraus.
Der Betrag des Vektor- oder Kreuzprodukts ist gleich der Fläche des Parallelogramms, das von den beiden Vektoren aufgespannt wird.
Sind diese beiden linear abhängig, liegen also auf derselben Geraden, ist die Fläche des Parallelogramms gleich Null. Das ist der Fall, wenn die Vektoren einen Winkel von 0° oder eines ganzzahligen Vielfachen von 180° zueinander bilden.
Willy
einfache version:
weil das skalarprodukt auch definiert ist über |a|*|b|*cos(winkel)
(dadrüber wird man üblicherweise auch den winkel zwischen 2 vektoren berechnen)
vorausgesetzt dass die vektoren a,b beide nicht gleich dem nullvektor sind,
dann folgt aus winkel=90° dass skalarprodukt=0 ist.
die umkehrung davon stimmt, genau genommen, nicht ganz.
Denn wenn skalarprodukt=0 ist, sagt dass nur dass der winkel gleich
90°+n*180° ist.
dass der winkel gleich 90° (also n=0) sein muss, ist damit nicht gesagt.
Realistisch betrachtet heißt diese drehung um 180° aber nichts anderes als:
wenn der winkel zwischen a un b 90° ist, dann ist der winkel
zwischen a und -b (alternativ -a und b)
90+180=270°
in 99% der fälle reicht die version, wie du sie da stehen hast.
Man kann das Skalarprodukt von Vektoren als eine Verallgemeinerung des Produktes gewöhnlicher reeller Zahlen auffassen. Für reelle Zahlen gilt ja etwa:
plus mal plus = plus , plus mal minus = minus
minus mal plus = minus , minus mal minus = plus
Für Vektoren (die in beliebige Richtungen z.B. in der Ebene oder im Raum zeigen können) definiert man nun:
a * b = |a|*|b| , falls die Vektoren a und b in die gleiche Richtung zeigen
a * b = - |a|*|b| , falls die Vektoren a und b in entgegengesetzte Richtungen zeigen (d.h. wenn der Winkel zwischen a und b gleich 180° ist)
Um nun, ausgehend von dieser Definition eines Produktes, die nur in Spezialfällen passt, zu einer damit verträglichen, aber allgemein gültigen Definition zu kommen, kommt die Cosinusfunktion ganz gelegen, da diese stetig ist und die speziellen Werte cos(0°) = 1 und cos(180°) = -1 hat.
Nun definiert man eben (noch durch wesentliche weitere Argumente gestützt) das Skalarprodukt von zwei Vektoren a und b durch:
a * b := |a| * |b| * cos(phi)
wobei phi der Winkel zwischen den Vektoren a und b ist. Natürlich wird dann a * b = 0 , wenn phi ein rechter Winkel mit cos(phi) = 0 ist.
Lax gesprochen: eigentlich ist es ja genau anders herum.
Man hat eine Beziehung zwischen Vektoren definiert, die in der Lage ist, den Winkel zwischen ihnen zu beschreiben (wie sonst eine Winkelfunktion). Und diese Definition wird gerade dann 0, wenn ein rechter Wnkel erreicht wird.
Da ist also überhaupt nichts Geheimnisvolles dran.
Aber es erleichtert den Umgang mit Vektoren kolossal.
könntest du mir eventuell noch erklären, weshalb das Vektorprodukt dann bei 0° bzw. 270°, also wenn die Vektoren aufeinander liegen, gleich 0 ist, um diese Fragen für mich endgültig abzuschließen? :) Wäre sehr nett