Vektoraufgabe?
Hallo, ich weiß leider nicht, wie ich die Aufgabe a lösen soll. Für b und c habe ich bereits einen Lösungsweg (bei b Betrag von Vektor AB mal 20, bei c Winkel berechnen durch Cosinusfunktion). Habe aber bei A überhaupt keine Ahnung, wusste nicht wo ich anfangen soll

3 Antworten
Hello... ich schlage dir folgende Lösung vor
wir drehen und verschieben das Koordinatensystem. Wir drehen es so, dass die neue Achse x* mit der Verbindungslinie vom Startpunkt zum Turm zur Deckung kommt. Dann verschieben wir das System so, dass der neue Koordinatenursprung im Startpunkt liegt.
Die Projektion der Seillinie auf unser neues System (x* Achse) ergibt eine Länge von
Wurzel ((220-20)^2 + (420-20)^2) = 447m (Pathagoras)
In diesem System haben wir dann das Steigungsdreieck des Seils:
x*=447m / y*=80m
Das ergibt die GeradenGleichung y* = 80/447 * x*
Auf dieser Geraden fährt der Kollege also nach oben.
Nun die Stützen:
Die Koordinaten ändern sich genau wie oben
Stütze 1: 70,120 das wird 50,100 Daraus x* = 111,8
Stütze 2: 120/220 das wird 100 / 200 x* = 223,6
Stütze 3: 170/300 das wird 150 / 280 x* = 317,6
x* sind die Stützpunkte der Säulen.
die nötige Höhe bekommen wir aus der Geradengeichung oben
y*stütze 1 = 80/447 * 111,8 = 20m (ist: 20m ist ok)
y*stütze 2 = 80/447 * 223,6 = 40,0m (ist: 30m ist nicht ok)
y*Stütze 3 = 80/447 * 317,6 = 56,8m (ist: 60m ist nicht ok)
Wir erkennen, dass nur die 1. Stütze passt, die andern müssen verschoben oder verlängert werden.
Wenn du sie verschieben willst, dann gehst du in die Geradengleichung und suchst für die jeweiligen Länge das passende x. als z.B. für Stütze 2: 30m = 80/447*x
x-Stütze 2 = 167m
Die Skizze ist nicht ganz richtig, deshalb ist es verwirrend bei Aufgabe a glaube ich.
80m ist der Turm hoch. Die Stützen sind 20, 30 und 60m hoch. Das sieht, wenn du es dir richtig aufzeichnest, komisch aus.
Was du herausfinden sollst ist was die Entfernung vom Stützen-Standpunkt bis zum idealen diagonalen Seil ist. Und dann vergleichen wie es in Realität aussieht und ob die Stützen kürzer oder länger sein sollten.
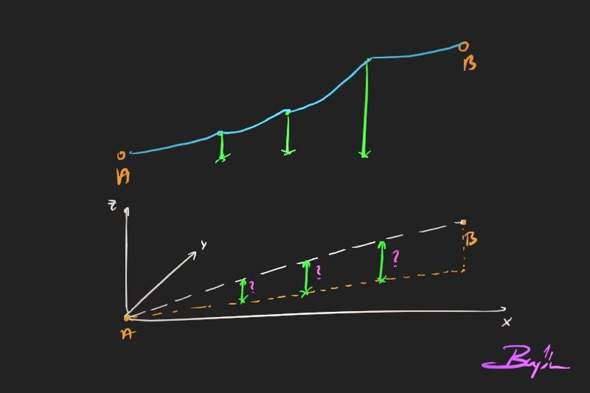
Was du also suchst sind die Längen der grünen Vektoren unten. Die Punkte/Ortsvektoren am Boden hast du ja gegeben. Einfach die z-Koordinate 0 setzen bei allen Stützen.
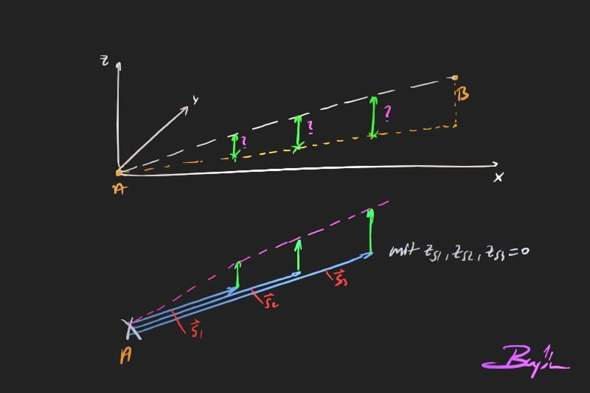
https://www.youtube.com/watch?v=K6ZCP8cpCc8
(Passt nicht 100% zur Aufgabe da dein projizierter Vektor "a auf b" bereits gegeben ist, aber die Informationen sollten dir trotzdem weiterhelfen)
Kleiner Fehler meinerseits: Der Startpunkt ist nicht der Nullpunkt sondern A. Das müsstest du noch anpassen. Also Statt direkt die Vektoren S bei z=0 zu nehmen musst du das gleiche Spiel mit den Vektoren von AS1 AS2 AS nehmen. Also die Vektoren in der Unteren Skizze sind AS1, AS2 und AS3. Nicht S1, S2 und S3.
Der Weg das auszurechnen klingt erstmal kompliziert ist es aber eigtl nicht. Man kann es auch auf andere Art und Weise berechnen aber du meintest ja Vektorrechnung :)


hello . . . weclhe Grundlagen habt ihr schon.... das ist letztlich eine Geradengleichung im Raum. Oder zeichnerisch, ist allerdings unhandlich wegen der großen Maßunterschiede