Trigonometrie Textaufgabe mit Tiefenwinkel korrekt gelöst?
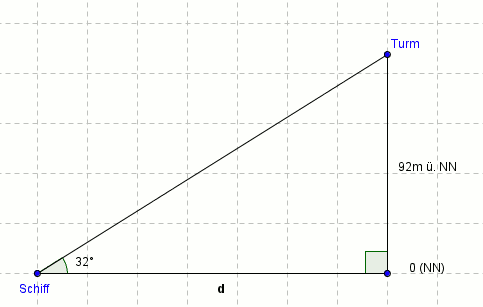
Von der Aussichtsplattform eines Leuchtturmes, der 92 m über NN hoch ist, erscheint ein Segelschiff mit dem Tiefenwinkel von 32 Grad.
Wie weit ist das Schiff vom Leuchtturm entfernt?
Gegeben:
Alpha = 32 Grad
Höhe bzw. a= 92
Ansatz:
Sin (Alpha)= a/c |*c
Sin (Alpha)* c= a |:sin(Alpha)
c= a/sin(Alpha), also
c= 92/Sin(32)
c~ 173,6 m
173,6 m ist die Entfernung des Schiffs. Danke für eure Hilfe und Mühe!
2 Antworten
Hallo,
mit der Entfernung zum Leuchtturm ist die Strecke Leuchtturmfuß (F) - Schiff (S) gemeint, nicht Aussichtsplattform (A)- Schiff (S).
Der Tiefenwinkel taucht als Wechselwinkel wieder beim Schiff auf, als Winkel FSA.
Der Winkel am Fuß des Leuchtturms SFA ist ein rechter Winkel.
Somit ist die Strecke FS die Ankathete, die Höhe des Leuchturms bis zur Plattform die Gegenkathete.
tan (32°)=Gegenkathete/Ankathete=92/FS
FS=92/tan (32°)=147,23 m
Herzliche Grüße,
Willy
Hallo,
ich verstehe die Aufgabe so:
d = tan(32°) = 92 / d => d = 92 / tan(32°) ≈ 132,23m
Gruß
Ups, danke. Da muss ich mich vertippt haben.
Ich habe noch einen kleinen Zweifel: wenn man es wörtlich nähme, wäre die Länge der Hypothenuse gefragt. Ich habe den Abstand des Schiffes zum Fußpunkt des Turmes berechnet.
Der Abstand Schiff-Turm "durch die Luft" ist ja uninteressant.
Wie siehst du das?
Gruß
Guten Abend,
Danke für Deine schnelle Antwort und Korrektur.
Ich habe dir eine Anfrage geschickt bzw. deine bestätigt; tut mir für die späte Antwort sehr leid.
Lg
Der Rechenweg ist korrekt, das Ergebnis nicht.
92/tan (32°)=147,2307767
Herzliche Grüße,
Willy