Sinus Kosinus Tangens?

Hallo, ich hab Mathehausaufgaben auf und so wie die da stehen haben wir die noch nie gemacht. Der Winkel ist irgendwie in der Mitte geteilt und ich verstehe nicht wie ich dann auf die Lösung kommen soll. Könnt ihr mir das bitte erklären?
Brauchst du hilfe bei dem Linken oder dem Rechten?
Beide leider
3 Antworten
Ohne Worte! 😂
Das ist eigentlich nicht weiter schwer.
Du kannst mit Pythagoras, weil die Höhe ja senkrecht steht, die fehlenden Seiten berechnen, und damit dann die beiden Teile des Winkels. Zusammenaddiert ist das dann der gesuchte Winkel! 😀
Bei der Aufgabe rechts gehst du genau andersherum vor: du berechnest einen Teilwinkel, dann mithilfe φ den anderen Teilwinkel und kommst so auf die gesuchte Seite.
Außerdem ist ja nicht der Winkel gesucht, sondern Seite A
OK, es ist zwar mMn albern, dass man Pythagoras nicht antwenden darf, aber man kann das auch in mehreren Schritten über die Winkelfunktionen machen.
Z.B. bei der linken Aufgabe:
- Den Teilwinkel γ, der von b und h eingeschlossen wird, ich nenne den jetzt mal γ₁, ergibt sich als Arkuskosinus aus b und h.
- Jetzt kannst du mit γ den anderen Teilwinkel γ₂ ausrechnen und mit γ₂ kannst unter Zuhilfenahme des Kosinus mit h dann a ausrechnen.
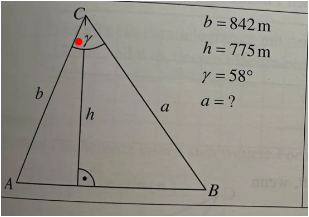
Ok. Das erste, also das linke habe ich mir bereits angeschaut. mal sehen ob ich das so erklären kann das du es verstehst. Damit wir mit Sinus, Cosinus und tangenz rechnen können brauchen wir ein rechtwinkliges Dreieck. Also ein Dreieck mit rechtem Winkel. Da die rechte seite des Dreiecks ein kleines dreieck mit rechtem winkel ist, ist das linke kleine dreieck im großen Dreieck auch ein rechtwinkliges. Jetzt haben wir oben bei C den Winkel des ganzen Dreiecks, das sind die 58° die vorgegeben sind. zudem haben wir die Seitenlängen von b=842m und h=775m. Wenn wir jetzt ausgehend von dem Winkel ob bei C des kleinen Dreiecks links im Großen Dreieck schauen, dann ist b die Hypothenuse des Dreiecks und h die Ankathete. Das heißt wir benötigen den Cosinus und können damit den linken teilwinkel oben bei C berechnen. Ich weiß nicht ob ihr soetwas auch hatte aber wir habuns das mit einem Merkspruch gemerkt: Sinus, Cosinus und Tangenz nebeneinander auf ein Blatt schreiben und darunter G für Gegenkathete, A für Ankathete und dann wieder G für Gegenkathete. Und darunter dann H für Hypothenuse, dann noch einmal H für Hypothenuse und A für Ankathete. So das am Schluss dann da steht: Sinus und darunter G und darunter H, so weißt du dann um den Sinus zu berechnen must du die gegenkathete durch die Hypothenuse teilen. (Wenn du dazu noch fragen hast versuche ich dir das später mit Bildern besser zu erklären).
Ok also wo waren wir. Teilwinkel oben in der linken Ecke bei C berechnen. Also wir haben dan Cos von C = h geteilt durch b. Also musst du in den Taschenrechner eingeben: Cos hoch -1 (775/842) dann sollte da gerundet 23° rauskommen. Jetzt hast du den Teilwinkel oben in C, den ziehst du einfach vom gesammt winkel ab: 58°-23°=35° jetzt hast du den teilwinkel vom rechten kleinen Dreieck. Nun brauchen wir wieder den Cos um die länge der Seite a herauszufinden. in demfall rechnen wir dann cos(35°)=a/775 Also machen wir auf beiden seiten mal 775 und erhalten dann gerundet 635m als lösung für a.
Wenn irgendetwas unklar war, melde dich einfach noch mal. Ich schaue mir kurz die zweite Aufgabe an :)
Vielen vielen Dank für deine Mühe. Ich hab’s verstanden. Zumindest die Aufgabe. Ich brauch manchmal immer so ein Denkanstoß bei so neuen Aufgaben, weil ich nicht weiß weil wenn ich einmal weiß wie man das rechnen kann Ich das auch vielen vielen Dank ich hab da jetzt schon so lange dran gesessen
Kein Problem :) weißt du wie du die zweite Aufgabe angehen musst? Sonnst kann ich dir für den anfang einen Tipp geben und dann kannst du schauen ob du weißt wie du weiter machen musst.
Ich weiß nicht so recht, ob ich das verstehe. Also ich hab jetzt erst mal den Teilwinkel von Den Winkel an P berechnet da hab ich 37,9 8° raus also ist der auf der anderen Seite 64,8 2° oder und jetzt versuche ich irgendwie die nicht gegebene Seite auszurechnen im Dreieck PRS damit ich dann mit dem Teilwinkel von P irgendwie X ausrechnen kann. Aber ich verstehs nicht so recht.
Ja genau. Mit dem Winkel 37,98° und der Seite u kannst du jetzt die Höhe berechnen. Also die Strecke zwischen P und S.
Ich hab jetzt weiter gerechnet. Hab als Ergebnis für X 12,03. Stimmt das?
Ja :) zumindest habe ich das auch raus bekommen. haha aber freut mich wenn ich dir helfen konnte :)
links
a lässt sich nicht direkt bestimmen. einzwischenschrittnotwendig
.

erstmal den Teil gam1 von Gamma mit
cos(gam1) = h/b
also cos^-1 ( 775/842)
.
mit 58 - gam1 erhält man gam2 und kann mit cos(gam2) = h/a zu a kommen.
.
.
..
..
rechts auch erst den Winkel RPS mit sinus und v und u
Darf man nicht man muss Sinus Cosinus tangens anwenden
wär schön wenn’s so gehen würde darf man aber nicht