Rotationskörper und ihr Volumen?

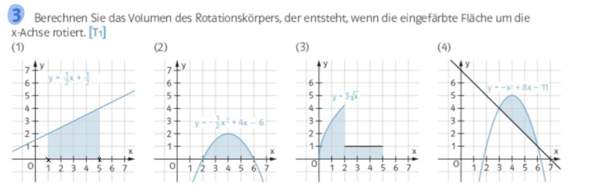
Kann mir bitte jemand mit den Aufgaben helfen, komme einfach nicht weiter. Habe das Thema gar nicht verstanden.. :/

Answer 1

[evtldocha]

Alles, was man zur Berechnung des Rotationsvolumens, das sich bei der Rotation des Graphen von f(x) um die x-Achse im Intervall [a;b] ergibt, wissen muss, ist die Gleichung:

$V=\pi\ \int_{_a}^{^b}\left(f\left(x\right)\right)^2\ dx$

Beispiel 3.1: Intervall [1;5]

$f\left(x\right)=\frac{1}{2}x+\frac{3}{2};\ \left(f\left(x\right)\right)^2=\frac{1}{4}x^2+2\cdot\frac{1}{2}x\cdot\frac{3}{2}+\frac{9}{4}=\frac{1}{4}x^2+\frac{3}{2}x+\frac{9}{4}$

$V=\pi\int_{_1}^{^5}\left(\frac{1}{4}x^2+\frac{3}{2}x+\frac{9}{4}\right)dx\ =\pi\cdot\left[\frac{1}{12}x^3+\frac{3}{4}x^2+\frac{9}{4}x\right]_{_1}^{^5}=\pi\cdot\frac{112}{3}$

Probe mit der Formel für das Volumen eines Kegelstumpfs:

$V=\pi\cdot\frac{h}{3}\cdot\left(R^2+r\cdot R+r^2\right)$ $h=5-1=4;\ R=f\left(5\right)=4;\ r=f\left(1\right)=2$

Damit:

$V=\pi\cdot\frac{4\cdot\left(4^2+2\cdot4+2^2\right)}{3}=\pi\cdot\frac{4\cdot28}{3}=\pi\cdot\frac{112}{3}$

Comments

[mathe5279]

dankeschön!

[evtldocha]

@mathe5279

Oh my dear. Ich schreib' es extra in der Form hin, dass man die Herkunft aus einer binomischen Formel sehen kann und Du erkennst es trotzdem nicht.

(a+b)² = a²+ 2ab + b² und setze a=(1/2)x und b=3/2

[mathe5279]

@evtldocha

ja, hab es dann später gemerkt sorry..

Answer 2

[LUKEars]

bei Aufgabe 1 sollst du wohl zuerst die Nullstellen finden...

um dann das Volumen des Rotationskörpers von bla bis blub rauszufinden, gibt es diese Trick-Formel: $\pi\cdot\int_a^b\left(f(x)\right)^2 dx$

noch Fragen?

Woher ich das weiß: Studium / Ausbildung – Absolvent/Universität

Comments

[mathe5279]

okay dankeschön, und bei der aufgabe drei also die 3) wie berechnet man sowas? gleich also genauso oder anders, weil die figur sieht irgendwie komplex aus

[LUKEars]

@mathe5279

ist immer dasselbe... Grenzen finden... also die Stellen „a“ und „b“....

[Wechselfreund]

@mathe5279

Zwei Teilkörper berechnen.

[mathe5279]

@Wechselfreund

wie genau?

[LUKEars]

@Wechselfreund

du meinst, dass er 3(3) und 3(4) meint? ja... da hat man mehrere Körper... einmal zum Addieren und einmal zum Subtrahieren...

[Wechselfreund]

@mathe5279

von 0 bis 2 mit der angegebenen Funktion, der Rest ist ein Zylinder. Wenn du willst, geht das auch über Integration.

[LUKEars]

@mathe5279

welche Teilaufgabe meinst du denn?

bei 3(4) braucht man erstmal die Schnittstellen zwischen der Geraden und dem Rundlichen...

[mathe5279]

@LUKEars

könnt ihr es vllt lösen, damit ich es verstehe? also nur das 3.3) bitte

[Wechselfreund]

@LUKEars

Hatte ich vermutet...

[mathe5279]

@LUKEars

allgemein die aufgabe 3, aber gemeint habe ich 3.3 eigentlich

[LUKEars]

@mathe5279

manno... hab total schlecht gepennt... bei 3(3):

integriere von 0 bis 2: (9x dx)

und dann von 2 bis 5: 1 dx

[mathe5279]

@LUKEars

und bei der 3.4)?

[LUKEars]

@mathe5279

die Gerade ist g(x)=-x+7 und das Rundliche ist f(x)=-x²+8x-11

1. g(x)=f(x) führt auf die Stellen x=3 und x=6... oder?
2. und dann integrieren von 3 bis 6: ((f(x))² dx)
3. und dann integrieren von 3 bis 6: ((-x+7)² dx)
4. und dann (2.) minus (3.)

[mathe5279]

@LUKEars

hi, sorry für die störundg, unser lehrer kann einfach nicht gut erklären und ich hab das thema nicht so ganz verstanden.. bei der aufgabe 1. wäre dann V=pi * (4/3x^3-4x^2-1/2x^2) nach dem aufleiten? und dann halt erst die obere grenze einsetzen und dann die untere? habe ich das richtig gemacht also. 1. schritt hab ich die funktion hoch 2 gesetzt und dann fällt die wurzel bei 4-x weg und die klammer x-1 ist hoch 2 dann hab ich die klammer mit der binomischen formel berechnet also x^2-2x+1 und dann hab ich die klammer mit den 4-x mal gemacht? passt das? oder habe ich ein fehler gemacht? vielen dank im voraus

[mathe5279]

@mathe5279

ah ne sorry, ist falsch habe vergessen mit x zu multiplizieren also so: V=pi*integral oben 4 unten 1 und dann -x^3+6x^2-9x+4 richtig? und nach dem aufleiten kommt man zu dem ergebnis 27/4 * pi bzw. ca 21,21?

[LUKEars]

@mathe5279

hey...

1. kennst schon WolframAlpha?
2. erstmal das Quadrat: (x-1)²(4-x)
3. dann Klammern ausmultiplizieren... also: (x²-2x+1)(4-x)=4x²-8x+4-x³+2x²-x
4. zusammenfassen: -x³+6x²-9x+4
5. integrieren: -0,25·x^4+2x³-4,5·x²+4x
6. du hast dich da wohl tierisch verrechnet... oh... im nächsten Kommentar wird es besser... hast es richtig... WA sagt: Link
7. der Mathe-Lehrer hat es aber auch schwer, weil diese Art Mathematik eben schon ziemlich abstrakt ist... es geht da für mich nur noch um Muster-Erkennung und das Anwenden von Rechenregeln, bis es endlich so ist, wie es sein soll... :!