Wie soll ich hier vorgehen?
Hii!
Ich komme bei dieser Nummer absolut nicht weiter! Ich habe keine Ahnung wo ich das den Satz des Pythagoras verwenden kann:( Die Nummer 1a habe ich ganz einfach alleine gelöst, aber was ist der Rest?
Danke jetzt schon Mal!!
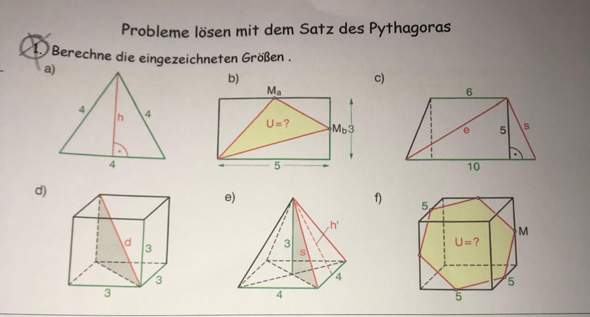
update: mir fehlt noch die d, e und f
2. Update: Mir fehlt noch die d und es wäre super nett wenn einer vielleicht dort die Rechen Schritte angeben könnte, da ich es nicht verstehe.
5 Antworten
Satz des Pythagoras lautet ja: a2+b2=c2 (hoch 2/zum Quadrat in dem Fall die 2) Ich helf mal bei denen die ich verstehe:
also bei c)
Die Diagonale ist gesucht, dadurch brauchen wir die 2 anderen Seitenlängen- unten steht 10 oben 6, 6 (die breite) wissen wir schon das ist aber nicht die ganze Länge, diese ist die Hälfte der Differenz zwischen 10 und 6 also 2. 6+2 ergibt 8, also ist das schonmal die untere Seitenlänge, die Höhe ist ja 5, und a Quadrat + b Quadrat ergibt c Quadrat, also a und b ist egal wie rum, aber 5 und 8 sind gegeben. Also 5 Quadrat sind 25 plus 8 Quadrat sind 64, daraus (89) die Wurzel weil wir c und nicht x Quadrat haben wollen, das sind 9,4. Das ist die fehlende Seitenlänge.
e) fehlen tut wieder eine Seitenlänge, die berechnet man mit der gegebenen 3 und der anderen Hälfte von 4, also 2. (3quadrat +2 Quadrat und daraus die Wurzel ziehen)
c)
Aus dem Trapez ergibt sich zwei Dreiecke 5*2.
Das Maß 2 erhältst du: ((10-6)/2)
s = Wurzel aus (5² + 2²)
e = Wurzel aus (6+2)² + 5²
e)
Für e) empfehl ich folgende Formelsammlung.
Formel 1 und 8 kommt da wohl in Frage.
http://texxtorr.bplaced.net/gf/Berechnungen/Pyramide/Viereckpyramide%20Formeln%20006.pdf
f)
Bei f) hat man ein Dreieck von 2,5*2,5.
Da ja auf halbe Länge von Seitenlänge des Würfels das Dreieck bewegt.
Hypothenuse = Wurzel aus 2,5² + 2,5²
Hypothenuse = 3,536
Hieraus kann man den Umfang des Sechseck berechnen.
Hypothenuse = 3,536 * 6
Bei b musst du erst die drei weisen dreiecke ausrechnen die punkte sind in der mitte 5/1,5 3/2,5 1.5/2.5
bei d musst du erst pythagoras an der unteren fläche anwenden das gleiche bei e
und f ist eine kombination
Das graue dreieck ist rechtwinklig wenn du die linie der unteren fläche berechnest dann hast du eine länge die andere länge ist die höhe 3 dann hast du 3^2*a^2=c^2
Hallo!
Tut mir leid falls ich dich nerve aber ich kann das nicht so nachvollziehen.
Also ich sehe das im grauen Dreieck sich oben ein rechtwinkliges Dreieck versteckt. Ich soll jetzt die Linie die sozusagen diese zwei grauen Dreieck trennt berechnen. Dann hab ich wie du auch meintest 3^2 • a^2 aber das ergibt doch nicht d^2? Weil da fehlt ja noch ein Stück? Oder bin ich blöd
Hallo, also du hast die Grundfläche von d) das ist ein Quadrat. Die Diagonale dazwischen(die graue line) kannst du mit dem Pythagoras Berechnen, da es im Prinzip zwei rechtwinklige Dreiecke sind mit den Seitenlängen von 3 so erhältst du eine Seite des grauen Dreiecks die andere Seite ist gegeben durch die höhe in dem Fall 3 so kannst du jetzt die Hypothenuse des grauen Dreiecks berechnen.
ich hoffe ich konnte das jetzt so erklären das du es verstehst.
Mathe ist sehr schwierig, dennoch lass den Kopf nicht hängen. Wenn du das noch ein bisschen übst hast du mit sowas bald keine Probleme mehr.
Ich drück dir die Daumen, lass dich nicht hängen und sag nicht das du blöd bist.
LG
Bei b sind um das gelbe Dreieck herum 3 rechtwinklige Dreiecke...
Ja stimmt! Danke! Dann muss ich von diesen Dreiecken jeweils die Hypotenuse berechnen und die dann für den Umfang zusammen addieren, richtig?
D) D soll für die seitendiagonale stehen
d für die Raumdiagonale
3*3+3*3=D*D
Wurzel18=D
18+18=36=d
Aber woher weißt du dass die andere Kathete auch D ist? Weil theoretisch müsste sie ja 3 sein wegen der Beschriftung.
bei der d) habe ich nun den Pythagoras an der unteren Fläche benutzt, aber das graue Dreieck ist ja gar nicht rechtwinkelig. Muss ich das graue Dreieck vielleicht in zwei aufteilen?