Pi = 4?
Den kannte ich noch nicht.
https://www.gutefrage.net/frage/was-waere-wenn-die-zahl-pi-doch-rational-waere#answer-515061869
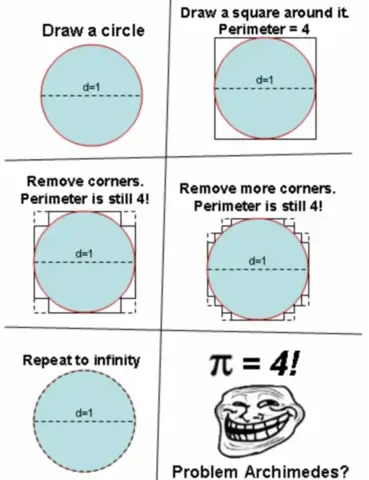
Der "Beweis" sieht ja recht plausibel aus. Wo genau ist der Fehler?
4 Antworten
Nur, weil sich die eckige Form immer mehr dem Kreis annähert, heißt das nicht unbedingt, dass sich auch der Umfang immer mehr an den eines Kreises annähert.
Allgemein muss der Grenzwert der Längen der Kurven zweier Folgen von Kurven nicht unbedingt gleich sein, wenn der Grenzwert der Kurven gleich ist.
Es bliebe sogar zu beweisen, dass sich das überhaupt einem Kreis annähert.
Jetzt dämmert es.
Eine ähnliche Problematik hat man bei der Messung von Küstenlinien oder anderen Grenzen.
https://www.spektrum.de/kolumne/kuestenlinien-paradoxon-eine-unbestimmbare-laenge/2002951
Eigentlich müsste ich ja jetzt meine Steuererklärung machen ...
Sei l(γ) die Länge einer rektifizierbaren Kurve γ. Seien
parametrisierte, rektifizierbare Kurven, wobei
gelte. Obwohl es bequem wäre, gilt dann allerdings
NICHT.
Ein Gegenbeispiel hast du dir selbst geliefert.
Es gilt aber, falls Differenzierbarkeit vorliegt,
allerdings gilt die Prämisse in diesem Fall natürlich nicht - allein schon wegen der Differenzierbarkeit, von der L^1 Konvergenz mal ganz zu schweigen.
Dasselbe kann man übrigens anwenden auf die Diagonale eines Quadrats: Diese entspricht in dieser naiven Vorgehensweise ebenfalls dem Doppelten der Seitenlänge. Das stimmt offenbar auch nicht.
So ist es.
Wie gesagt, es ist in diesem Fall schlicht die genannte Implikation, die erst bei Folgen stimmt, deren Ableitung in L^1-Norm konvergiert.
Ein Kreis ist dadurch definiert, dass alle Punkte den gleichen Abstand zum Mittelpunkt haben. Aus diesem Abstand (Radius) ergibt sich der Durchmesser als das Doppelte. Offensichtlich gibt es aber bei den Zwischenstufen jede Menge Punkte, die keineswegs den gleichen Abstand zum Mittelpunkt haben, woraus sich andere Radien und Durchmesser ergeben.
Ja, aber dass die so konstruierte Ersatz"kurve" sich einerseits an den richtigen Kreis anschmiegt und trotzdem um mehr als ein Viertel länger sein soll, sehe ich jetzt nicht auf Anhieb.
Der "Beweis" ist offensichtlich falsch, das weiß ich auch.
Er ähnelt der Erklärung des Integrals durch Ober- und Untersummen. Was ist der entscheidende Unterschied? Vermutlich die unterschiedliche Breite der "Annäherungsrechtecke."
Merke gerade beim Integral geht es nicht um Kurvenlängen ...
Ein Zeichnerischer Beweis ist kein Beweis. Denn es müßte zunächst gezeigt werden dass die Folge des "wegnehmens" tatsächlich gegen den Kreis konvergiert. Tut sie aber nicht, die Länge der vier den Kreis berührenden STrecken konvergiert nicht gegen 0.
Tante Edit sagt dass das noch genauer hier
http://infrastruct.blogspot.com/2012/05/why-pi-is-not-4-and-other-mysteries.html
begründet wird. Insbesondere sind die von der Zeichnung suggerierten kleinen Quadrate in Wirklichkeit gar keine.
..
Sah so ausals wenn dieser Kommentar an der falschen Stelle gelandet wäre. Sch... GF
Insbesondere sind die von der Zeichnung suggerierten kleinen Quadrate in Wirklichkeit gar keine.
Das ist es wohl. Wenn man kurz nachdenkt ...Danke.
Obwohl...
Warum müssen das Quadrate sein? Die Idee ist doch, dass ich in Manhattan an der gleichen Stelle herauskomme, wenn ich erst 3 Straßen nördlich und dann eine nach Westen gehe oder erst eine nach Westen und dann 3 Straßen nach Norden.
Ich schau mir deinen Link mal genauer an.
Damit diese Wegbetrachtung klappt müsste die Summe der Längen in die beiden unterschiedlichen Richtungen tatsächlich gleich sein. Sind sie aber eben nicht, zumindest nicht wenn man gleichzeitig den Kreis weiter berühren will.
Und da sieht man es auch sofort ein. Die Fläche unter dieser Ersatzkurve wäre aber wie bei der Diagonale das halbe Quadrat. Die Länge kann man so nicht annähern.