Physik-Aufgabe zur Corioliskraft - warum ändert sich der Winkel in Abhängigkeit von der Wurfrichtung?
Hallo zusammen, folgende Aufgabe. Laut Musterlösung sind a) und b) korrekt gelöst, für c muss man allerdings über sin(a) umstellen und daher alpha über den arcsin von w mal r durch v errechnen. Außerdem ist auch die Flugzeit nicht analog, sondern über t = R durch wurzel v quadrat minus w quadrat mal R quadrat gegeben. Ich verstehe nicht, weshalb das einen Unterschied macht, ob ich vom Zentrum aus nach außen werfe oder von außen ins Zentrum. Woher kommt plötzlich der trigonometrische Zusammenhang? Und warum brauche ich bei der Flugzeit plötzlich die Formel mit die Wurzel …? Was berechne ich da überhaupt genau? Danke schonmal für eure Antworten.


2 Antworten
Die "Coriolis-Kraft" ist nur eine Scheinkraft.
Der Ball fliegt in die Richtung, in die sich die Hand im Moment des Loslassens bewegt.
Von Max (angenommen, die Wurfhand ist exakt im Zentrum) wird sich der Ball praktisch radial nach außen bewegen. Für Katrin sieht das nicht so aus, weil sie sich selbst ja auch bewegt.
Von Katrin fliegt der Ball am Zentrum vorbei, wenn sie ins Zentrum zielt, da auch ihre Seitwärtsbewegung die Wurfrichtung (aus Sicht von Max) beeinflusst. Sie muss also quasi ein bisschen nach hinten werfen, damit der Ball zu Max kommt.
Betrachte die Situation jeweils in einem Inertialsystem (hast Du ja bei a) und b) bereits gemacht).
Bei c) hat Katrin die Tangentialgeschwindigkeit
Aus ihrer Sicht bewegt sich Max mit dieser Geschwindigkeit normal zur radialen Richtung (keine Kreisbewegung; Skizze machen). Soll der Ball Max erreichen, muss sie dies entsprechend berücksichtigen.
Es gelten die Gleichungen
Aus der 2. Gleichung folgt der gesuchte Winkel. Die Zeit folgt aus
---
Ergänzung: Nochmals zum Aufgabenteil c):
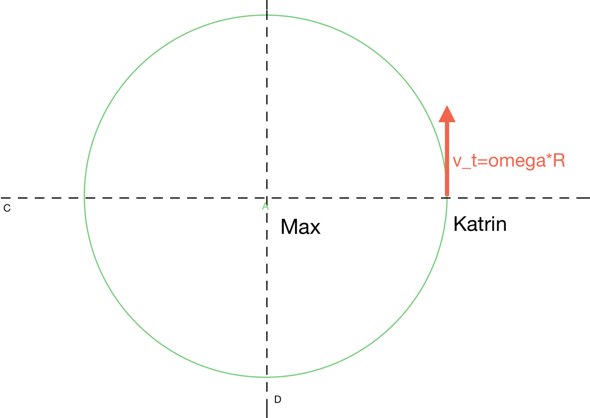
In einem Inertialsystem, in welchem der Mittelpunkt ruht, hat Katrin im Augenblick des Abwurfs die Geschwindigkeit v_t=omega*R.

Geht man über in ein Bezugssystem, in dem Katrin im Augenblick des Abwurfs ruht, hat Max die Geschwindigkeit v_t in entgegengesetzter Richtung, vgl. die nachfolgende Skizze.

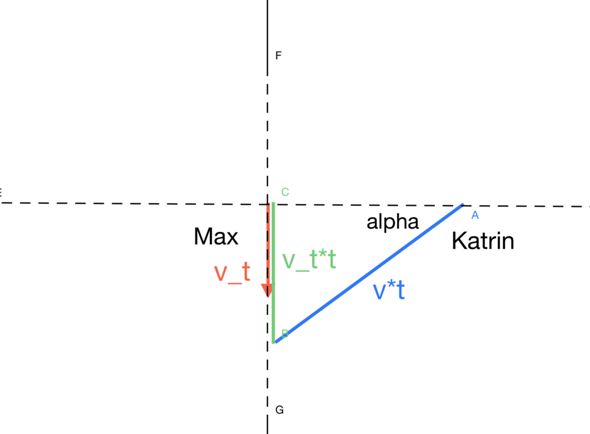
Da sich dieses Bezugssystem mit konstanter Geschwindigkeit v_t gegenüber dem ersten Bezugssystem bewegt, handelt es sich ebenfalls um ein Inertialsystem. Während des Wurfs legt Max in diesem Bezugssystem die Strecke v_t*t zurück. Katrin muss deshalb den Ball unter einem Winkel alpha zur Geraden, die im Zeitpunkt des Abwurfs Max und Katrin verbindet, abwerfen. Aus der Skizze ergeben sich die Gleichungen weiter oben.
Die beiden Situationen b) und c) sind nicht äquivalent, denn:
b): In einem Bezugssystem, in dem Max ruht, bewegt sich Katrin auf einer Kreisbahn. Dies muss er beim Abwurf berücksichtigen.
c): In einem Bezugssystem, in dem Katrin im Moment des Abwurfs ruht, bewegt sich Max geradlinig mit konstanter Geschwindigkeit v_t.
Ja, alpha ist der Winkel bei Katrin zwischen einer Geraden zum Zentrum im Augenblick des Abwurfs und der Wurfrichtung, mit welcher Max erreicht wird. Ich kann sonst morgen noch ausführlicher schreiben und allenfalls eine Skizze beifügen.
Ich glaube, ich bin gedanklich so langsam auf der richtigen Spur, aber wäre dir natürlich super dankbar, wenn du es morgen noch etwas ausführen könntest, falls das für dich nicht zu viel verlangt wäre :).
Ahh, hetzt habe ich es verstanden. Ich habe den Zusammenhang zwischen der Tangentialgeschwindigkeit von Katrin und Max‘ dazu relativer Position einfach nicht gecheckt. Aber jetzt ist es mir klar geworden. Vielen vielen Dank dir für die Hilfe :)))!
Also ist mein Winkel in der Überlegung auch falsch eingezeichnet, oder? Also müsste alpha an karins position liegen?