Wann arctan arcsin und arccos?
Hallo Leute.
ich verstehe das mit dem arcus nicht so ganz.
BSP:
Aufgabe: wandle die komplexe Zahl in die Polarform um.
was benötige ich also? R als Radius und den Winkel.
r berechne ich ja durch wurzel (a)^2 + (b)^2. für den Winkel wird nun mit arccos gerechnet. Ist das bei Winkeln (bez. Auf so eine Aufgabe ) immer so? Wann nehme ich arctan und wann arcsin?
ps: einen Taschenrechner darf ich nicht benutzen
3 Antworten
Hallo Eliifff,
"arcus" heißt Bogen. Der Winkel φ wird mit dem Verhältnis zwischen einem Kreisbogen zwischen den Schenkeln von φ und dem Radius des Kreises identifiziert.
Als kartesische Form würde ich
(1) z = x + i∙y
schreiben, mit
(2) |z| =: r = √{x² + y²}.
Für φ gilt
(3.1) cos(φ) = x⁄r
(3.2) sin(φ) = y⁄r
(3.3) tan(φ) = y⁄x
(3.4) cot(φ) = x⁄y;
Wenn x und y beide positiv sind, ist
(4) φ = arccos(x⁄r) = arcsin(y⁄r) = arctan(y⁄x) = arccot(x⁄y),
d.h., jede dieser Funktionen kannst Du benutzen, um φ auszurechnen (den Arcustangens habe ich hervorgehoben, weil ich ihn bevorzuge).
Die Funktionen haben einen eingeschränkten Definitionsbereich. Davon, welche Du benutzt, hängt es ab, wie Du vorgehen musst, sollte x, y oder beides nicht positiv sein.
Wenn Du den TR nicht benutzen darfst, werden Dir sicherlich nur Aufgaben gestellt, in denen spezielle Winkel vorkommen, z.B. ⅙π = 30°:
sin(⅙π) = ½
cos(⅙π) = √{¾} = ½√{3}
tan(⅙π) = 1/√{3}
wenn man den Wert des Tan ,Sin oder Cos hat , meinetwegen
cos(winkel) = 0.2610
Wie kommt man auf den Winkel ?
mit der Fkt arccos, die dem cosinuswert einen Winkel zu ordnet !
.
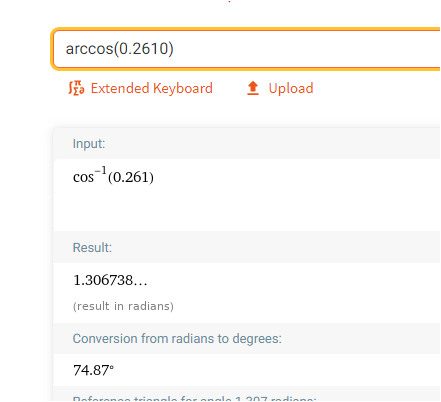
aber achtung : zu einem cos-Wert gehört nicht nur ein Winkel .
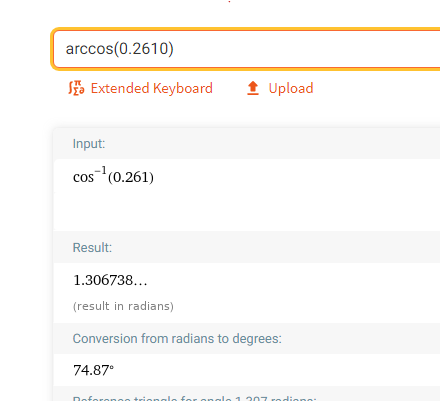
Wenn kein TR benutzt werden darf, dann vermutlich auch nicht Wolframalpha.
guckst du hier.
https://www.mathespass.at/klasse7/komplexe_zahlen_polarform.php
Das bringt mir nichts. Wie gesagt, ich darf keinen Taschenrechner benutzen daher bringt mir die Seite mit den gradzahlen auch nichts