mathematik hausaufgabe ich verstehe es nicht?
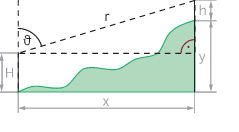
Die Höhe eines Hügels soll vermessen werden. Die Höhe des Messinstruments (Theodoliten) beträgt H=1,80m, die Höhe der Messlatte beträgt h=0,95m. Man misst r=423m und die ,,Zenditdistanz'' Winkel =55.83 grad. Berechne die waagrechte Entfernung x des Messinstruments von der Messlatte sowie die Höhe y des Lattenfußpunktes.
Ich verstehe die Angabe nicht kann mir das jemand erklären skizze siehe bild danke im foraus
5 Antworten
Du hast oben ein rechtwinkliges Dreieck.
ϑ kennst du, also kennst du auch den anderen Winkel, der mit ϑ einen rechten Winkel ergibt (90° - ϑ).
Anschließend wühlst du in deinem Gedächtnis ein bisschen und überlegst dir wie Sinus und Kosinus in einem rechtwinkligen Dreieck definiert sind.
Mit dem berechneten Winkel neben ϑ kannst du nun eine Gleichung aufstellen, die du nach x auflösen kannst, womit du dann y berechnen kannst. Und fertig. ;)
LG Willibergi
hallo willibergi ich habe fragen zum thema mathematik gestellt wollte dich fragen falls du zeit hast pb du mir die frage beantworten könntest wo die quadratische gleichung ist (mit bild) und die frage mit von einem nicht rechtwinkeligen dreieck kennt man die seite b sowie .. usw kannst du mir helfen wenn du zeit hast;) lg danke
also die fragen ,, wie soll ich das machen mathe''
,,mathe kann mir das jemand erkären''
Zusammen bilden
- die bekannte Strecke r (Hypotenuse),
- die unbekannte Strecke x (Ankathete) sowie
- die unbekannte vertikale Strecke (Gegenkathete, nennen wir sie mal z) vom rechten Ende von x zum Ende von r, also h+(y-H) ---> sieht man der Skizze
ein rechtwinkliges Dreieck.
Der uns bekannte Winkel ϑ stellt dabei den Ausgangwinkel dar, mit dessen Hilfe man den Sinus, Cosinus und Tangens berechnen kann.
Hier ( http://www.mathematik-wissen.de/trigonometrie.htm ) ist das gut erklärt, der Winkel α dort entspricht dem Winkel ϑ in deiner Aufgabe.
Der Sinus von ϑ gibt das Verhältnis Gegenkathete/Hypotenuse an, also:
sin(ϑ) = z/r ---> ϑ und r ist uns bekannt
sin(55,83) = z/423
0,8274 = z/423 --> beide Seiten mal 423
z = 349,9795
Wir wissen (aus der Skizze), dass:
z = h + (y - H) ---> uns ist h, H und z bekannt
349,9795 = 0,95 + (y - 1,80)
(y - 1,8) = 349,0295
y = 350,83
Die Höhe des Lattenpunktfußes y ist also 350,83m.
Um jetzt noch x zu berechnen, einfach den Satz des Pythagoras anwenden, denn r (Hypotenuse) und z (Gegenkathete) sind bekannt.
a² + b² = c²
x² + z² = r²
x² + 349,9795² = 423²
x² = 423² - 349,9795²
x² = 178929 - 122485,6504 = 56443,3496
x = 237,5781
Die waagerechte Strecke x ist also 237,5781m lang.
Du hast ein rechtwinkliges Dreieck gegeben sowie die Hypotenuse r und den Winkel Theta und sollst nun die Entfernung berechnen. Was machst du nun wohl? Trigon....
also wenn ich cos von winkel * radius rechne habe ich das y oder?
dann hab ich x aso aber wie rechne ich x aus
Theta liegt in einem 90° Winkel.
Rechne also 90-Theta, dann hast du den Winkel von dieser Spitze.
x hast du ja schon berechnet, r ist gegeben.
Sorry, hab was vergessen: Du hast dann nur das Stück vom Dreieck, dazu musst du noch "H" addieren.
ah und dann mit dem winkel muss ich y ausrechnen
Für y, ja. Zusätzlich musst du für die Höhe noch H addieren.
aber das x stimmt nicht weil da kommt mir was anderes raus aber es soll 349.98 rauskommen
Das habe ich doch gerade geschrieben.
Gib dir doch selbst erst mal Mühe und zeig deinen Ansatz zur Lösung. Das ist keine schwierige Aufgabe.
Gegeben sind die Hypotenuse r und (indirekt) der linke Winkel, ich nenne ihn mal Beta, des rechtwinkligen Dreiecks.
Beta + der gegebene Winkel ergeben 90°; also weißt Du wie groß Beta ist.
An x kommst Du über den cos, indem Du cos(Beta)=x/r nach x umstellst. Setzt Du nun die gegebenen Werte ein, erhältst Du auch den Wert Deiner Musterlösung. Entsprechend dann die Gegenkathe über den sin ausrechnen, und dann mit diesem Wert und der Werte H und h das y ermitteln.
es muss laut lösungen rauskommen x= gerundet: 349,98 und y ist gerundet 238,43
Danke für den Stern! ;)
LG Willibergi