Mathe Aufhabe?
Kann mir bitte jemand dabei helfen?
Ich habe gerade Pythagoras und verstehe diese Aufgabe nicht.

Es geht um die Aufgabe oben.
3 Antworten
(Habe die falsche Aufgabe gemacht)
DB = AB – AD
DB = 14 cm – 4 cm = 10 cm
.
DC² = AD • DB (Höhensatz: h² = p • q)
DC = √(AD • DB)
DC = √(4 cm • 10 cm) = 2√10 c
.
BC² = DB² + DC² (Pythagoras: c² = a² + b²)
BC = √(DB² + DC²)
2 r = √((10 cm)² + (2√10 cm)²)
2 r = 2√35 cm
r = √35 cm
.
A_Kreis = π r²
A_Kreis = π (√35 cm)²
A_Kreis = 35 π cm² ≈ 109,96 cm²
.
A_Dreieck = 1/2 G h
A_Dreieck = 1/2 • AB • DC
A_Dreieck = 1/2 • 14 cm • 2√10 cm
A_Dreieck = 14√10 cm² ≈ 44,27 cm²
.
Maßstabsgetreu sieht die Abbildung übrings so aus:
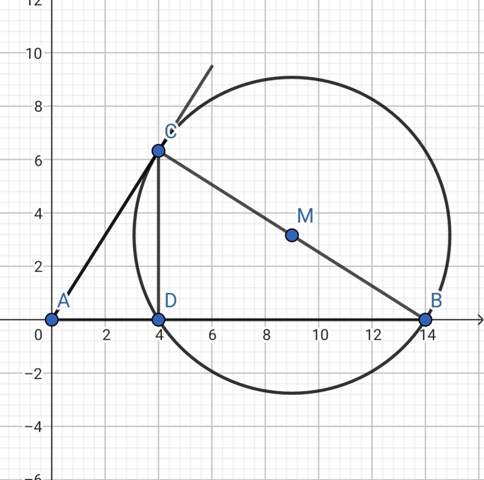

Da das Dreieck gleichseitig ist,
beträgt jeder Winkel im Dreieck 60°
---
Weil gleichseitig läßt sich
Winkel β wie folgt berechnen
β = (90 - α) / 2
β = (90 - 60) / 2
β = 15°
---
Geg.: a = 10 mm ; β = 15°
Ges.: s
s = a / COS(β)
s = 10 / COS(15)
s = 10,352762 cm


Ja ja das kostet normalerweise Geld.
Hab das mal vor einigen bei youtube gefunden. 😉
Hab das auch in meiner ehemaligen Firma verwendet.
Aber wenn du was kostenloses willst, empfehle "Autodesk Fusion 360".
Das gibt es kostenlos für Hobbyanwender. Da kann man ähnliche Sachen machen.
Hallo,
jedes Quadrat hat eine Innenwinkelsumme von 360°.
Sprich 90 ° pro Ecke.
Vorteil hier ist, dass es sich um gleichseitiges Dreieck handelt.
also 60 ° und 15 ° jeweils für die anderen Dreiecke.
Verwende den Cosinus
10/cos(15)= 10,35 (Länge der Seite)
Gruß
Vorteil hier ist, dass es sich um gleichseitiges Dreieck handelt
Wie kommst du darauf?
Wie kommst du darauf?