Wie komme ich auf die Gleichung der Parallelen in Abhängigkeit von a, wenn a der SP von f(x) und p ist?
Hallo,
ich habe eine Matheaufgabe, zu der ich eine Frage hätte.
Die Aufgabe lautet:
Eine Parabel mit der Gleichung f(x)= -x^2+9 begrenzt mit der x-Achse eine Fläche. Bestimme die Gleichung einer Parallelen zur x-Achse, die diese Fläche in zwei gleich große Teile teilt.
Überlegt hatte ich mir:
Der Inhalt der gesamten Fläche ist 36 (mit 2x integral im Intervall 0-3 ermittelt)
Also ist die Hälfte 18.
Somit könnte man rechnen: 18= 2x Integral von (f(x) - die Parallele in Abhängigkeit einer Variablen (a)) im Intervall 0-3.
a selbst soll der Schnittpunkt von Parallelen und Funktion sein.
Genau da hänge ich jetzt irgendwie.
Entschuldigt die seltsame Schreibweise. Ich weiß nicht, wie man hier Funktionen korrekt schreibt.
3 Antworten
du meinst doch parallele zur x-Achse??
dann
parallele einzeichnen und nur rechtes stück betrachten;
a • f(a) + integral f(x) in den grenzen a und 3 = 9
und a berechnen. dann f(a)
erst ist die fläche unter dem Graph 72 weil sie durch die x-achse und nicht durch die x- und die y-achse beschränkt ist.
Wie komme ich auf die Gleichung der Parallelen in Abhängigkeit von a?
Es gilt ganz einfach für die gleichung der Parallelen:
ich bin mir eigentlich ziemlich sicher, dass die Fläche 36 ist. a soll die Stelle sein, an der sich die Parallele und f schneiden. Hatte ich vergessen zu sagen. Und in der Abhängigkeit dieses SP möchte ich die Parallelengleichung
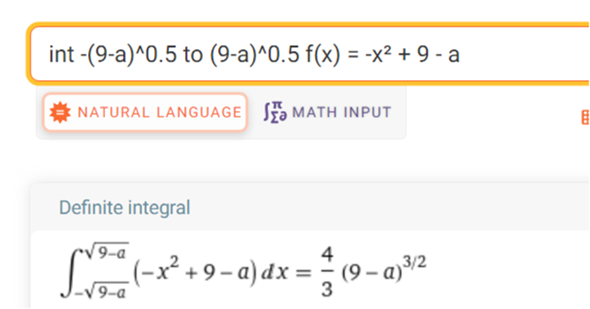
die Fläche zwischen y = a und Parabel soll 18 sein
Daher
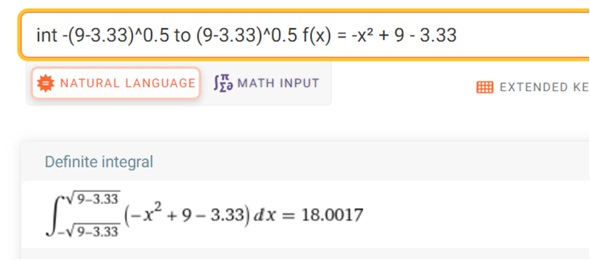
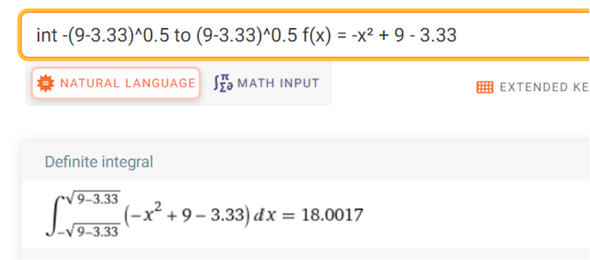
int -x² + 9 - a
.
aber von wo bis wo ?
von schnittpunkt bis schnittpunkt
es gibt schnittpunkte mit y = a
.
a = -x² + 9
x² - 9 + a = 0
x1 , 2 = + - wurz(9-a)
.
sieht dann so aus
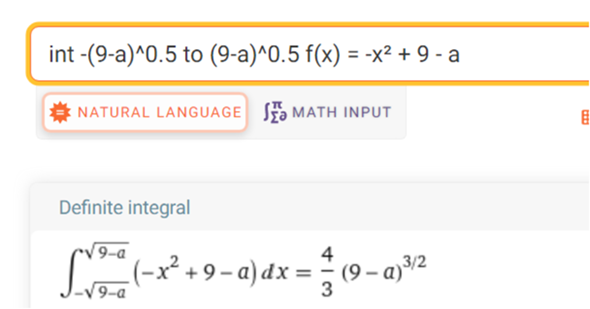
nun den rechten Term = 18 setzen und a bestimmen.
Der Wert a = 3.330355 passt , denn Parabel unten breiter als oben . Muss unter 9/2 = 4.5 liegen.
.
Kontrolle