Mathe---Hilfe?
Hey Leute, Aufgabe 2 konnte ich noch lösen, jedoch komme ich bei 3 und 4 nicht weiter. Es wäre sehr nett, wenn mir da jemand helfen könnte.

LG
Aufgabe 4;

4 Antworten
Aufgabe 3)
Zuerst berechnen wir die Geraden u und v:
u: x = (2/-2/3) + r(-4/2/-2)
v: x = (2/0/0) + r(-2/3/3)
Und nun werden aller Geraden nacheinander und miteinander geschnitten. Das ist eine Fleißaufgabe.
1) g und h:


2) g und u:

3) g und v
4) h und u
5) h und v
6) u und v



Eine Gerade besteht aus einem Stützvektor und einem Richtungsvektor. Als Stützvektor nimmt man man den Ortsvektor des ersten Punktes (= dessen Koordinaten) sowie dem Richtungsvektor von diesem Punkt zum anderen Punkt.
Den Richtungsvektor berechnet man, indem man von den Koordinaten des 2. Punktes die des 1. Punktes abzieht.
Richtungsvektor u = D - C = (-2/0/1) - (2/-2/3) = (-4/2/-2)
Damit:
u: x = (2/-2/3) + r(-4/2/-2)
Theoretisch könnte man den Richtungsvektor auch noch mit 2 kürzen, sodass rauskommt:
u: x = (2/-2/3) + r(-2/1/-1)
Das ist dann dieselbe Gerade, bloß dass sich halt bei beiden Schreibweisen r unterscheidet.
Im Prinzip hat man für die Gerade zwei Vektoren aneinandergereiht. Mit dem Stützvektor kommt man vom Urspung zum Punkt 1 und mit dem Richtungsvektor von Punkt 1 zu Punkt 2. Dadurch, dass man vor den Richtungsvektor das r setzt, das einen beliebigen Wert annimmt, verlängert man sozusagen den Richtungsvektor nach vorne und hinten beliebig lange, sodass dadurch aus dem Richtungsvektor die gesuchtre Gerade wird.
Da Vektoren ja an sich beliebig verschiebbar sind, ohne ihren Wert zu ändern, legt man den nach hinten und vorne zur Geraden beliebig verlängerten Richtungsvektor durch die Angabe des Stützvektors die Gerade im Koordinatensystem fest. Sie muss dann durch den ersten Punkt gehen.
Vielen lieben Dank! Bei Aufgabe 4 habe ich das nicht so ganz verstanden, kannst du mir vlt jeweils bei den Aufgaben sagen was zu tun ist😅
Zu Aufgabe 4 hatte ich bereits was in einem Extrabeitrag geschrieben. Hast du das gesehen?
Soll ich das besser in einer neuen Fragestellung hochladen?
Nein, wir könnnen unter dem Kom zu Aufgabe 4 weiterschreiben. Was genau hast du nicht verstanden? Den Lösungsweg habe ich ja aufgezeigt.
Ist es richtig, dass bei b die Geraden windschief sind?
Aufgabe 4b
A(6/8/0)
G(0/0/4)

B(0/8/0)
H(6/0/4)

Nun schneiden wir die beiden Geraden:


Das Ergebnis ist keine Überraschung. Die Raumdiagonalen eines Quaders schneiden sich in dessen Mitte. Die Koorodinaten dieser Mitte sind dann natürlich genau die Hälfte von Breite, Länge und Höhe.
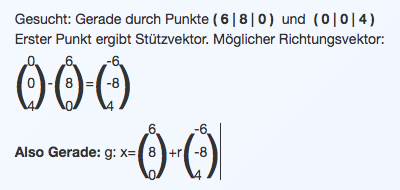
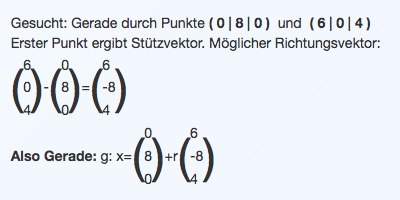


Genau so habe ich es auch berechnet, habe bei jedoch bei r -0,5 erhalten, ich weiss nicht, was ich faslch gemacht habe. Bei s habe ich auch 0.5 raus
Wie bist du auf Ia und Ib gekommen? Habe Schwierigkeiten, deinen Rechenweg nachzuvollziehen.
Unten hast du m.E. einen Vorzeichenfehler.
II 1. Zeile: -(-8 * 0,5)
sollte in II zweite Zeile zu +4 und nicht -4 führen (Minus mal Minus = Plus)
Okay, habe mein Fehler gesehen, jetzt bekomme ich auch 0.5 raus, vielen Dank!
Aufgabe 4)
Das Koordinatensystem ist vorgegeben mit dem Ursprung in F.
x = breite
y = Tiefe
z = Höhe
Nun stelllen wir die Koordinaten der einzelnen Punkte auf, z.B.
A(6/8/0)
G(0/0/4)
Und legen die Gerade durch die beiden Punkte:
gAG: x = (6/8/0) + r(-6/-8/4)
Dito alle anderen Punkte und Geraden.
Dann kann man die gewünschten Geraden schneiden und deren Lage zueinander feststellen.
Wie genau hastdu die Gleichung aufgetellt und wie macht man es bei bh?
Die Geradengleichung habe ich so aufgestellt, wie ich es bei Aufgabe 3) genauer erklärt habe.
Was ist bh?
Da gibt es eine Gleichung die GBH genannt wurde
Dazu ermittelst du zuerst die Koordinaten von B und H. Das musst du einafch aus der Zeichnung ablesen.
Dann legst du die Gerade durch B und H, indem du B als Stützvektor nimmst und den Richtungsvektor vob B nach H ausrechnest.
Achso okay, eine Frage wegen der 3. Aufgabe, müssen alle Geraden parallel oder schneiden sein, denn ich erhalte auch windschiefe
Wenn rechnerisch windschief rauskommt, ist das halt so. Dann sind die Geraden weder parallel noch schneiden sie sich.
aber ich habe Angst, dass ich es falsch gerechnet habe
Bei Aufgabe zwei lohnt sich ein Blick auf die Richtungsvektoren der Geraden. Sind diese gleich (oder kolinear, falls das der richtige Begriff war), so verlaufen die Geraden parallel. Wenn sie nicht parallel sind, dann schneiden sie sich bei einem gemeinsamen Punkt. Die Berechnung ist dann wie bei Aufgabe 1.
Bei Aufgabe 4 gibt's auch nicht viel anderes zu tun, als bei den anderen Aufgaben. Nur du musst erst Geradengleichungen selbst herstellen.
LG
Wenn sie nicht parallel sind, dann schneiden sie sich bei einem gemeinsamen Punkt.
Wenn sie sich eine gemeinsame Ebene teilen. Anderenfalls sind sie windschief.
Laufen die Geraden nicht parallel, müssen sie sich nicht unbedingt schneiden, sondern können einfach aneinander vorbeilaufen (Stichwort: windschief)!
Eine Frage, wie hast du u und v ausgerechnet?