Laurent-Reihe?

Was ist die Laurent-Reihe/Reihendarstellung von: 1/(1+x^5) bei x=unendlich

Answer 1

[LORDderANALYSE]

Theorie

Mit den Formeln zur Laurent-Reihe, erhalten wir die Lauren-Reihe:

bzw.

Durchführung

Für die Laurent-Reihe um x = unendlich erhalten wir damit:

als PNGs:

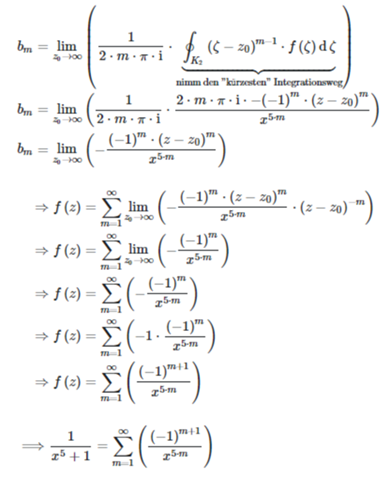
als LaTeX-Code:

$$
\begin{align*}
&\text{Mit den Formeln von Laurent}\\
&\quad f\left( z \right) = \sum_{m = 0}^{\infty} \left( a_{m}\cdot (z - z_{0})^{m} \right) + \sum_{m=1}^{\infty} \left( b_{m} \cdot \left(z - z_{0} \right)^{-m} \right)\text{,}\\
&\quad a_{m} = \frac{1}{2 \cdot m \cdot \pi \cdot \mathrm{i}} \cdot \oint_{K_{1}} \frac{f\left( \zeta \right)}{\left( \zeta - z_{0} \right)^{m + 1}} \operatorname{d}\zeta\\
&\text{und}\\
&\quad b_{m} = \frac{1}{2 \cdot m \cdot \pi \cdot \mathrm{i}} \cdot \oint_{K_{2}} \left( \zeta - z_{0} \right)^{m - 1} \cdot f\left( \zeta \right) \operatorname{d}\zeta\\
&\text{erhalten wir für } z_{0} :\to \infty \text{:}\\
&\quad a_{m} = \frac{1}{2 \cdot m \cdot \pi \cdot \mathrm{i}} \cdot \oint_{K_{1}} \underbrace{\lim_{z_{0} \to \infty} \frac{f\left( \zeta \right)}{\left( \zeta - z_{0} \right)^{m + 1}}}_{\text{Nenner geht gegen } -\infty \text{, also geht der Term gegen } 0} \operatorname{d}\zeta\\
&\quad a_{m} = \frac{1}{2 \cdot m \cdot \pi \cdot \mathrm{i}} \cdot \underbrace{\oint_{K_{1}} 0 \operatorname{d}\zeta}_{\text{bestimmtes Integral von } 0}\\
&\quad a_{m} = \frac{1}{2 \cdot m \cdot \pi \cdot \mathrm{i}} \cdot 0\\
&\quad a_{m} = 0\\
\\
&\qquad \Rightarrow f\left( z \right) = \sum_{m = 1}^{\infty} \lim_{z_{0} \to \infty} \left( b_{m} \cdot \left(z - z_{0} \right)^{-m} \right)\text{,}\\
\\
&\quad b_{m} = \lim_{z_{0} \to \infty} \left( \frac{1}{2 \cdot m \cdot \pi \cdot \mathrm{i}} \cdot \underbrace{\oint_{K_{2}} \left( \zeta - z_{0} \right)^{m - 1} \cdot f\left( \zeta \right) \operatorname{d}\zeta}_{\text{nimm den "kürzesten" Integrationsweg}} \right)\\
&\quad b_{m} = \lim_{z_{0} \to \infty} \left( \frac{1}{2 \cdot m \cdot \pi \cdot \mathrm{i}} \cdot \frac{2 \cdot m \cdot \pi \cdot \mathrm{i} \cdot -\left( -1 \right)^{m} \cdot \left(z - z_{0} \right)^{m}}{x^{5 \cdot m}} \right)\\
&\quad b_{m} = \lim_{z_{0} \to \infty} \left( -\frac{\left( -1 \right)^{m} \cdot \left(z - z_{0} \right)^{m}}{x^{5 \cdot m}} \right)\\
\\
&\qquad \Rightarrow f\left( z \right) = \sum_{m = 1}^{\infty} \lim_{z_{0} \to \infty} \left( -\frac{\left( -1 \right)^{m} \cdot \left(z - z_{0} \right)^{m}}{x^{5 \cdot m}} \cdot \left(z - z_{0} \right)^{-m} \right)\\
&\qquad \Rightarrow f\left( z \right) = \sum_{m = 1}^{\infty} \lim_{z_{0} \to \infty} \left( -\frac{\left( -1 \right)^{m}}{x^{5 \cdot m}} \right)\\
&\qquad \Rightarrow f\left( z \right) = \sum_{m = 1}^{\infty} \left( -\frac{\left( -1 \right)^{m}}{x^{5 \cdot m}} \right)\\
&\qquad \Rightarrow f\left( z \right) = \sum_{m = 1}^{\infty} \left( -1 \cdot \frac{\left( -1 \right)^{m}}{x^{5 \cdot m}} \right)\\
&\qquad \Rightarrow f\left( z \right) = \sum_{m = 1}^{\infty} \left( \frac{\left( -1 \right)^{m + 1}}{x^{5 \cdot m}} \right)\\
\\
&\quad \Longrightarrow \frac{1}{x^{5} + 1} = \sum_{m = 1}^{\infty} \left( \frac{\left( -1 \right)^{m + 1}}{x^{5 \cdot m}} \right)\\
\end{align*}
$$

Woher ich das weiß: Studium / Ausbildung – Mathematikstudium