Konvergiert oder divergiert diese Folge und falls sie konvergiert gegen welchen Grenzwert?
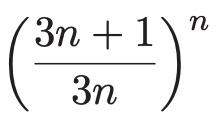
Konvergiert oder divergiert diese Folge und falls sie konvergiert gegen welchen Grenzwert? Ich versuche es zu verstehen, aber es geht nicht. Kann jemand helfen?
2 Antworten
Das ist (1 + 1/(3*n)) ^ n.
Wir substituieren 3*n = t
(1 + 1/t) ^ (t/3)
Der Grenzwert von (1 + 1/t)^t ist e, also ist die Folge konvergent. Der gesuchte Grenzwert ist e^(1/3) (etwa 1,4).
Hallo,
der geht gegen e^(1/3)=1,395612425 (gerundet).
Beweis:
Forme den Term in der Klammer zu (1+1/(3n)) um und den ganzen Term zu
e^[n*ln (1+1/(3n))].
Wenn Du den Limes in den Exponenten ziehst, berechnest Du nun den Limes für n gegen unendlich von n*ln (1+1/(3n))=ln (1+1/(3n))/(1/n).
Da sowohl Zähler als auch Nenner gegen 0 gehen, kannst Du nun die Regel von de l'Hospital anwenden und die Grenzwerte der Ableitungen berechnen.
Diese lauten für den Zähler 1/(1+1/(3n))*(1/3)*(-1/n²) und im Nenner -1/n², was sich gegen -1/n² im Zähler kürzen läßt, so daß für die Grenzwertberechnung der Limes von n gegen unendlich von (1/3)*1/(1+1/(3n)) bleibt.
1+1/(3n) geht für n gegen unendlich gegen 1.
So bleibt als Limes (1/3)*1=1/3.
Da wir den Limes in den Exponenten gezogen hatten, haben wir als endgültigen Grenzwert e^(1/3).
Herzliche Grüße,
Willy
Als Definition von e fällt mir normalerweise die Taylor-Reihe von e^x, entwickelt an der Stelle x = 0, berechnet für x = 1 ein. Aber die Aufgabenstellung legte die "alte" Definition nahe.
Darüber habe ich mir (ehrlich gesagt) keine Gedanken gemacht.
An l'Hospital hatte ich auch gedacht, das aber nicht auf Anhieb hinbekommen und dann lieber die "klassische" Definition von e rausgeholt.