Können Punkte im Raum nicht eigentlich immer auf allen Ebenen sein?
Hi, bei Aufgabe 6 stehen ja die Punkte den jeweiligen Ebenen zugeordnet. Aber ist es nicht eigentlich so, dass zB Punkt S auch auf der x1 x2 Ebene liegt?
4 Antworten
Das macht einen Unterschied. Z.B. Punkt U liegt in der x1x3 Ebene also musst du von diesem Punkt aus einen senkrechten Strich zur x1-Achse denken und das ist dein Koordinatenwert für die x1-Achse.... wäre es die x2x3-Ebene müsstest du senkrecht zur x2-Achse nach oben gehen
Genau deshalb sind ja die ebenen angegeben...
Da du bei der zweidimensionalen Projektion des dreidimensionalen Koordinatensystems nicht erkennen kannst, wo genau der Punkt liegt.
Mit der Angabe, auf welcher Ebene der Punkt liegt, ist das allerdings schon möglich...
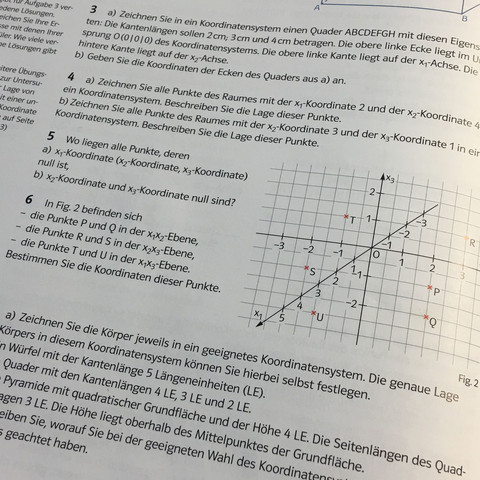
Aus der zweidimensionalen Abbildung (Projektion) des dreidimensionalen Raums ist nicht zu sehen, in welchen Ebenen die Punkte liegen. Das wird in Aufgabe 6 als zusätzliche Information gegeben, nur dann ist es möglich, die Koordinaten der Punkte aus der Abbildung abzulesen.
Also kann man die Punkte nicht ablesen „wie man will“? Weil S könnte ja zB (2 | -1 | 0) sein aber auch (0 | -2 | -1)
Es sollte aber erwähnt werden, dass es ohne Angabe der ebene unendlich viele Möglichkeiten gibt...
Damit es der FS besser versteht...
Denn er scheint es ja im Grunde verstanden zu haben...
Und mit der Bestätigung, dass er gewissermaßen richtig lag, wird das Gelernte besser aufgenommen, da man besser lernt, wenn man das Gefühl hat, richtig gelegen zu haben...
Nein. Es ist doch ausdrücklich gesagt, dass er das nicht tut.
Nein, die Aufgabe gibt eben vor, dass S in der x2-x3-Ebene liegt, also x1 = 0 ist. Durch die Angabe der Ebene gibt es immer nur eine Möglichkeit.