Kann mir hier jemand helfen?
Wir haben in Mathe Aufgaben zum lösen bekommen, diese verstehe ich aber nicht wirklich. Könnte mir jemand bei diesen helfen?


Wäre wirklich echt lieb, wenn jemand helfen könnte 🥹
Danke an alle, die auf die Frage geantwortet haben. Es macht jetzt so ein bisschen mehr Sinn und ich versuch's weiter alleine ^^
3 Antworten
Ich gebe Dir mal einen Ansatz zu
Erstmal etwas theorie:
Diese Gleichung enthält x² als kleinsten Koeffizienten und nichts dahinter. Daraus ergibt sich schonmal eine Aussage: Die Graph ist entlang der y-Achse weder nach oben noch nach unten verschoben und muss daher in x=0 eine Nullstelle besitzen.
Weiterhin gilt (für alle Zahlen im R Raum) bei Funktionen des 3. Grades, dass so eine Funktion MAXIMAL drei Nullstellen haben kann. Die Aufgabe sagt ja, dass hier nur zwei Nst vorhanden sind. Das passt perfekt zur ersten Aussage, dass keine Verschiebung entlang der y-Achse vorhanden ist. Denk mal an eine Parabel (x²) die nach oben oder unten verschoben sein kann je nach Verschiebung kann diese 2,1 oder keine Nst. haben.
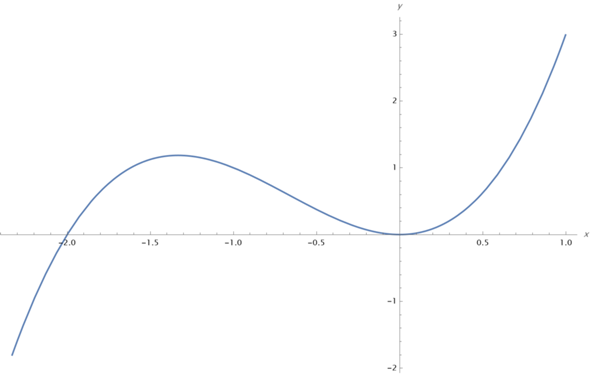
Mit einer Skizze könntest Du zum einen beweisen, dass die Funktion nur zwei Nst hat: Man erhält so etwas:

Da nach der 2. Nst bei 0 der Graph nur noch streng monoton steigend ist (oder auch dort ein Extreum hat) kann danach keine Nst mehr kommen; umgekehrtes gilt für x=2, dort MUSS mindestens eine Nullstelle folgen, da erst nach der Nullstelle der Graph wieder fällt.Hier ist wichtig, dass Du kurz begründest, wie das Steigeungsverhalten kurz vor oder hinter der Nst ist.
Die andere Variante (kürzere), ist die, die "DerRoll" schon angesprochen hat: rechnerisch lösen.
Ich kann bei der Funktion den niedrigsten Summanden (und Koeffizieten) ausklammern:
nun setze ich den Term für f(x)=0
es gilt der Satz des Nullproduktes:
Ein Produkt wird insgesamt Null, wenn einer der Faktoren den Wert Null annimmt. Anders formuliert: Es ist egal ob Du 100000 mal 0 hast oder 0 oder 88888 - in beiden Fällen ist das Ergebnis Null weil einer der Faktoren null ist.
Gleiches gilt für den obrigen Fall:
x²=0 ist einfach x=0
und x+2=0 nun das kann man sich an einer Hand abzählen
Folglich sind die einzig beiden Nullstellen:
Was genau verstehst du denn nicht? Da das Thema Exponentialfunktionen ist solltest du bereits aus der Zeit der ganzrationalen Funktionen wissen was eine Ableitung ist und was die Ableitung ausdrückt. Berechne also die Ableitung am Punkt x = 0 und du hast die Tangentensteigung. Weiter berechne den Funktionswert der Funktion für x = 0 und du hast den y-Achsenabschnitt der Tangente. Damit kannst du die Geradengleichung aufstellen.
Für die b) benötist du Integralfunktionen. Zeichne zunächst die Fläche grob ein und überlege dir welcher Parameter die Flächengröße bestimmt. Nun verwende die Integralfunktion um auf den gesuchten Flächeninhalt von 1,5 zu kommen und mach dann die Zeichnung "richtig", indem du den so berechneten Parameter korrekt einsetzt.
Für die zweite Aufgabe klammere x² aus und verwende den Satz vom Nullprodukt. Dann integriere von Nullstelle zu Nullstelle.
Für die dritte Aufgabe überlege dir erstmal welchen Wert die Ableitung an lokalen Extremstellen hat. Damit kannst du bestimmten welcher Graph die Ableitung sein muß (Hinweis: Der durchgezogene). Für den zweiten Teil verwende wieder die Integralfunktion.
Sorry, aber Nachhilfe kann dir hier niemand geben, das funktioniert nicht remote und deine Hausaufgaben wird dir auch keiner erledigen.
Ich mach mal die erste Aufgabe.
diese verstehe ich aber nicht wirklich.
Dann werde ich die Fragen stellen, die du dir selber stellen müsstes und werde auch die passenden Antworten dazu geben.
Bestimmen Sie die Gleichung der Tangente
Was für eine Funktion ist eine Tangente?
Das ist eine Gerade
Wie lautet der Ansatz für eine Gerade?
y = my + b
Wieviele Unbekannte hat die Geradengleichung?
zwei, nämlich m und b
Wieviele Informationen benötigt man, um die zwei Unbekannten zu lösen?
Genauso viele, nämlich 2.
Welche Informationen kann man dem Text entnehmen?
a) Die Tangentem geht durch den Schnittpunkt der Funktion mit der x-Achse. Dieser Schnittpunkt ist also ein Punkt auf der Geraden
b) Die Steigung der Tangente hat dieselbe Steigung wie der Graphen von f an dieser Stelle, sonst wärs ja keine Tangente.
Wie gehts jetzt weiter?
Wir müssen zuerst mal rauskriegen, wo dieser ominöse Schnittpunkt liegt:
Bestimmung des Schnittpunktes S von f(x) und y-Achse:
Welche Eigenschaft hat ein Punkt auf der y-Achse?
Es gilt immer: x = 0
Wir rechnen:
f(0) = 2 * e^(-0,5 * 0) = 2 * e^0 = 2 * 1 = 2
Damit haben wir die Koordinaten von S:
S(0/2)
Bestimmung der Steigung in S:
f'(0) = -e^0 = -1
Damit haben wir den Ansatz für die Tangente:
y = -1 * x + b
y = -x + b
b ermitteln wir, indem wir die Punktprobe mit S machen, also die Koordinaten in die Tangentengleichung einsetzen:
2 = -0 + b
b = 2
Und damit lautet die Gleichung der Tangente:
y = -x + 2
0 = 2e^(-0,5)
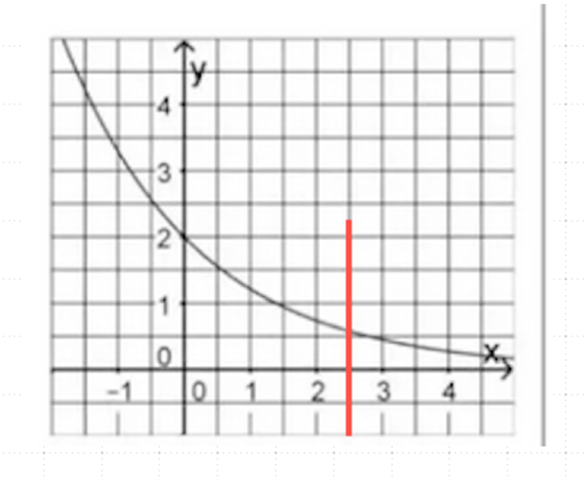
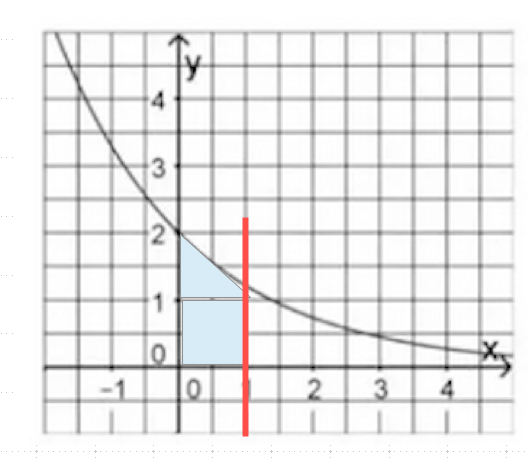
b) Da muss man sich das Bild angucken und im Geiste etwas rumprobieren, um die Flöäche von 1,5 hinzukriegen. Wenn man das nur in der Vorstellung nicht schafft, muss man halt ein bischen rummalen und vor allem erstmal versuchen zu verstehen, von welchen Linien die Fläche begrenzt sein soll. Da hilft eine Skizze weiter:

Da ist der rote Strich aber wohl zu weit rechts. Eine Fläche von
A = 1 * 1 = 1 hat 4 Köstchen. Wir brauchen für A = 1,5 also 6 Kästchen, die in der Fläche liegen.
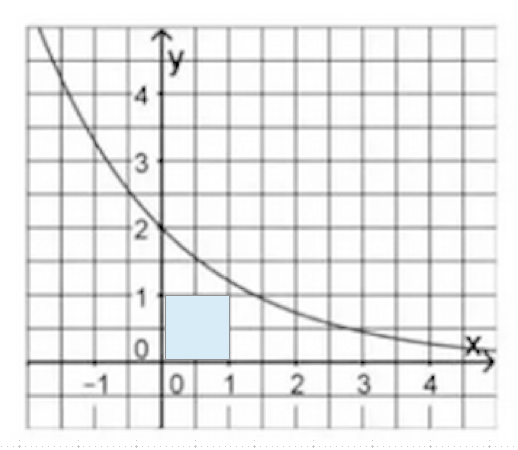
Zuerst zeichnen wir am besten mal A = 1 ein:

Und schon sehen wir: über dem Quadrat liegen zusammen nochmal 2 Kästchen:

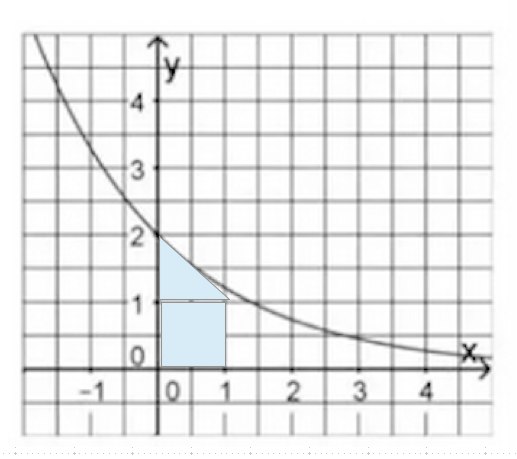
Das können wir also mit einem Dreieck annähern. Nun wissen wir auch, wo wir die Parallele zur y-Achse einzeichnen können:

Jetzt haben wir also A = etwa 1,5.
Da die Fläche aus einem Quadrat und einem Dreieck besteht, können wir die Fläche leicht berechnen:
A = 1 *1 + 1/2 * 1 * 1 = 1 + 0,5 = 1,5
Ding ist, egal wie viel man mir das erklärt, ich komm damit nicht wirklich klar. Selbst schon die Ableitungen mach ich da komplett falsch wenn da nicht ein Teil doch mal richtig sein sollte
Aber trotzdem danke für die Antwort ^^