Ich komm bei dem Sudoku nicht weiter, kann jemand helfen?
Bitte erklär mal wie du das lösen würdest.
7 Antworten
Das ist eigentlich sehr einfach weil die möglichen Zahlen bereits vorgegeben sind.
Du musst darauf achten, dass sich die Zahlen von 1-9 Senkrecht, Waagerecht und im Kästchen nicht wiederholen.
So, nun hast du ganz unten, rechts in einem Kasten zwei leere Felder. In beiden besteht die Möglichkeit, entweder 3 oder 4 einzusetzen. Wenn du jetzt aber Senkrecht nach oben schaust siehst du das in einem nur die 4 möglich ist, folglich kommt die 4 ins zweite Kästchen unten Rechts und ins erste Kästchen ganz oben rechts, die 6 daneben.
Die 3 füllt dann unten, den Kasten aus. Da sie sich ja nicht wiederholen darf, kommt die drei logischerweise in dem Kasten, oben rechts an erster Stelle.
Nun kannst du den Kasten auch ausfüllen weil ja nur noch eine Zahl fehlt.
Und so machst du weiter bis alle Felder ausgefüllt sind.
Viel spass 😉
Ps: Komplizierter wird es wenn die möglichen Zahlen nicht vorgegeben sind, oder wenig bis keine Start zahlen da sind das Prinzip ist aber das selbe. Die Zahlen dürfen sich einfach nicht wiederholen.
nicht wiederholen
sorry, ich verstehs leider nicht aber trotzdem danke
Hallo,
manchmal kommst Du nur durch Probieren weiter.
Dazu suchst Du Dir am besten Kästchen, in denen nur zwei Zahlen möglich sind.
Wenn Du Dir die Zeile 9 ansiehst, kann die 7 nur in Spalte 4 oder 5 stehen.
Setzt Du sie probehalber in Spalte 4 ein, führt dies im weiteren Verlauf zu einem Widerspruch, weil in Zeile 6 die 6 zweimal auftaucht.
Also gehört die 7 in Spalte 5 der Zeile 9.
Das ist schon der Schlüssel.
Ab hier kommst Du ohne weiteres Probieren ans Ziel.
Herzliche Grüße,
Willy
probieren würde ewig lange dauern, das kann man nicht im kopf machen. das geht sicher eleganter
99% der sodukos basieren auf schlichtem probieren bzw. notieren welche zahlen in jenes feld reinpassen.
hast du alle felder abgecheckt, dann guckst du mal überall, in jeder zeile, spalte oder feld, welche nummer nur in einem der felder vorkommt.
so muss man sich nahc und anch vorarbeiten.
wie sollen sonst harte sudokus funktionieren bei denen insgesamt nur 3 oder 4 felder vorgegben sind? :O
Blödsinn. Manchmal kommst Du um das Probieren nicht herum. Nach ein paar Minuten bist Du dann entweder fertig oder hast einen Widerspruch gefunden, der Dich dann zur richtigen Lösung führt.
ich löse sudokus auf experten stufe im schnitt in 15 minuten.
bist du sicher? ich glaube es muss doch irgend eine teilmengen aisschließung geben oder so
Ich hatte mir vor ner Weile mal eine Excel-Tabelle geschrieben, mit der man die gängigen Prinzipien an Vorkommen rausfinden kann. Das ist hier aber alles nicht der Fall.
Das einzige, was man noch eingrenzen kann, ist dass in Spalte 1 im mittleren Quadrat 3,8,9 vorkommen muss. Das kann also in den restlichen fünf Feldern dieses Quadrats nicht mehr auftauchen. Somit muss die 3 in einem der beiden Felder der 2. Spalte und die 8 in einem der beiden Felder der 3. Spalte im unteren Quadrat stehen.
Insgesamt sieht das dann so aus, wenn man in rot alle Möglichkeiten zu den bisher bekannten schwarzen Zahlen einträgt:
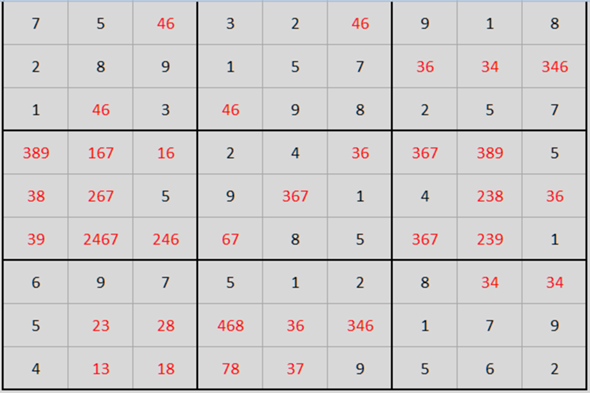
Da weiß ich aber jetzt auch leider nicht mehr, als sich ein Feld, wo nur zwei Zahlen drinstehen herzunehmen und es da mal mit der ersten Zahl zu versuchen. Entweder läuft das dann sauber bis zum Ende durch, dann war die Zahl richtig. Oder man erzeugt irgendwann einen Widerspruch, dann muss es die andere Zahl gewesen sein.
Vielleicht gibt es irgendwo noch ne Möglichkeit mit noch krasseren Herangehensweisen, das doch noch systematisch lösen zu können. Aber da weiß ich jetzt auch keine davon.
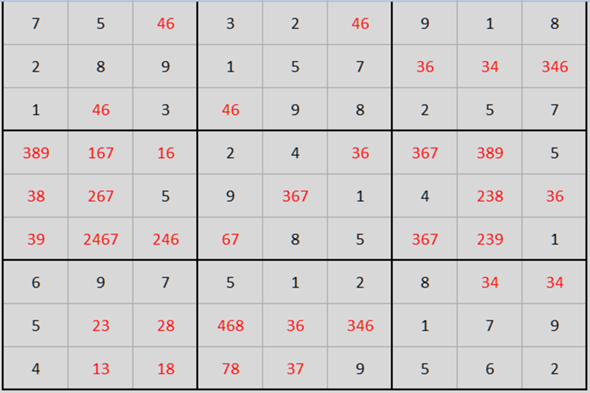
Die 3 in der vorletzten Spalte kann man übrigens aus den mittleren drei Feldern noch entfernen, da im obersten und untersten freien Feld nur 3 oder 4 stehen kann und die 3 somit im mittleren Quadrat in dieser Spalte nicht mehr vorkommen kann. Hatte ich oben vergessen.
Sechste Zeile von oben 2. Kästchen von rechts ist die "9".
Da sind noch felder wo dir noch keine nummern notiert hast :-)
Vielleicht ergibt sich ja dadurch noch was Hübsches?
Stimmt so nicht, der FS hat nicht alle hilfszahlen eingetragen. Oben rechts sind 3,4,6 noch frei, wo unten also die 4 hin kommt ist nicht ersichtlich.