Hilfe in Mathe (Thema Potenzen)?

Ich schreibe bald eine Klassenarbeit und verstehe das Thema absolut nicht. Hier sind ein paar Aufgaben die mir genannt wurden, die drankommen werden. Kann das mir jemand erklären wie ich das am besten rechnen kann?

Vielen Dank!

Comments

[verreisterNutzer]

verstehe das Thema absolut nicht

... heißt was genau?

[zitronene1stee]

Wo ich anfangen soll, was für Regeln ich anwenden soll und wann und wann es genug vereinfacht ist.

Answer 1

[Halbrecht]

Potenzgesetze anwenden . Findet man im Buch oder im Netz

dazu kommen die Basics . Bruchrechnung und Quadratzahlen

Potenzregel :::::::::::: x^a * x^b = x^(a+b) oder rückwärts

und wissen das 5^-2 = 1/5² oder 1/x^-4 = x^4

x^(n-2) = x^n * x^-2
x^-2 kürzen
5*x^(-1 - - 2) = 5^x(-1+2) = 5x^1 = 5x

.

x^2n = x^n * x^n
x^n kürzen
x^(n+1 - n) = x^1 = x

.

damit ist der Nenner überall x^n 

3x/x^n - 5x/x^n + x/x^n 

Zusammenfassen möglich , weil derselbe Nenner.

(3x-5x+x)/x^n 

=

-x/x^n

=

-1/x^(n-1)

oder = 

- x^(1-n)

.

Probe mit Rechenmagd

.

bei

muss man schon einen Plan haben. Es ist wahrscheinlich ,dass im Zähler auch (x-1) steckt .

(x-1)² = x² - 2x + 1
wie kommt man z.b auf die + 1 ? ? ? ........man klammert x^(n-1) aus ( probeweise ) und schaut

x^(n-1) * ( x² - 2x + 1 ) 

kommt hin .

Comments

[zitronene1stee]

Vielen lieben dank!

Answer 2

[gauss58]

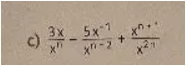
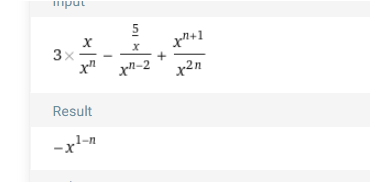
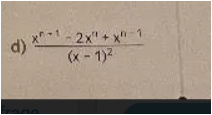
Hier geht es darum, Potenzregeln anzuwenden und Binome zu erkennen. Ein Beispiel:

21a)

(x^(2n) - 121) / (x^(2n) + 22x^n + 121) =

((x^n)² - 11²) / ((x^n)² + 2 * 11 * x^n + 11²) =

Zähler: 3. Binom, Nenner: 1. Binom

((x^n - 11) * (x^n + 11)) / (x^n + 11)² =

(x^n - 11) / (x^n + 11)

Comments

[zitronene1stee]

Vielen Dank erstmal! Aber wie genau kamen Sie jetzt von  (x^(2n) + 22x^n + 121) zu ((x^n)² - 11²) wenn ich fragen dürfte?

[gauss58]

@zitronene1stee

Du vergleichst hier den Nenner des ursprünglichen Terms mit dem Zähler des umgefornten Terms. Das geht nicht.

Ich habe Zähler und Nenner jeweils separat umgeformt.

Zähler:

(x^(2n) - 121) =

Es gilt: x^(2n) = (x^n)² und 121 = 11²

(x^n)² - 11² =

Drittes Binom anwenden:

(x^n - 11) * (x^n + 11)

Nenner:

(x^(2n) + 22x^n + 121) =

Es gilt: x^(2n) = (x^n)² und 22x^n = 2 * 11 * x^n und 121 = 11²

(x^n)² + 2 * 11 * x^n + 11² =

Erstes Binom anwenden:

(x^n + 11)²

Nach diesen Umformungen kann man (x^n + 11) im Zähler und Nenner kürzen.

[zitronene1stee]

@gauss58

Dankeschön für diese Ausführliche Erklärung.