Hallo, ich habe ein paar Fragen zum Transformator?
Also erstmal voraus, ich weiß wie ein Transformator aufgebaut ist, ich kenne seine Funktionsweise und ich weiß wie er funktioniert!
Okay also klar ist, wenn an die Primärspule eine Wechselspannung angelegt wird, dann entsteht ein veränderliches Magnetfeld. Denn jede Stromdurchflossene Spule baut ein Magnetfeld um sich auf. So dieses veränderliche Magnetfeld wird fast vollständig auf die Sekundärspule übertragen, durch einen geschlossenen Eisenkern. So und durch das Verhältnis der Windungszahlen an der Primär und Sekundärspule kann dann die gewünschte Spannung erzeugt werden.
So meine Frage ist:
Also wenn es ja so ist, dass in einer Spule eine Spannung induziert wird solange sich das von der Spule umfasste Magnetfeld verändert wird und die Spannung auch noch umso größer ist je schneller das Magnetfeld verändert wird und je höher die Windungszahlen sind, dann ist meine Frage:
Ist die induzierte Spannung auch umso höher, je höher die angelegte Wechselspannung ist?
Dies gilt jetzt in einer einzigen Spule, nicht in einem Trafo.
Dann noch eine Frage, die ist so ähnlich:
Wenn ich an einer Spule mit 1000 Windungen eine Wechselspannung von 6V anlege, dann entsteht ein veränderliches Magnetfeld. Aber wie groß ist denn hier die induzierte Spannung? 6V?!?
Danke für die Antworten!
4 Antworten
der Spitzenwert der Wechselspannung ist nicht entscheidend, aber die Frequenz! Da wie du ja schon richtig erkannt hast, die Änderung des magnetischen Flusses und somit auch der Stromstärke eine Rolle spielt
Wieso wird sie denn nicht größer? Das Magnetfeld verändert sich doch dann schneller und dann ist die Spannung größer oder nicjt?
Von U(primär) auf Fluss wird integriert. Kommt ein Faktor 1/ω.
Von Fluss auf U(sekundär) wir differenziert, da kommt ein Faktor ω.
1/ω * ω = 1
==> Die Frequenzabhängigkeit hebt sich auf.
Doch, der Scheitelwert der Spannung ist auch wichtig.
Bei gleicher Frequenz bedeutet ein höherer Scheitelwert der Spannung automatisch einen steileren Anstieg.
Wenn der Scheitelwert bzw. Effektivwert der Eingangsspannung doppelt so groß ist, ist auch die induzierte Spannung auf der Sekundärseite doppelt so groß.
Umgekehrt wird die sekundäre Spannung aber nicht größer, wenn man die Frequenz vergrößert, denn es kommt so rüber.
Nur zur Klarstellung.
Also ist es quasi egal wie viel Volt ich an der Wechselspannung habe? Denn das war eigentlich meine Frage, ob die Volt Anzahl die Frequenz beeinflusst, denn dann wäre die induzierte Spannung stärker
rickm 1988, Comment0815:
Das ist leider völlig daneben. Dann würde ein Transformator frequenzabhängig übertragen, also die Kurvenform verändern, wenn sie nicht sinusförmig ist. Tut er aber nicht.
...solange du ihn nicht in die Sättigung treibst... indem du ihn z.B. statt bei 50Hz an 16,7Hz betreibst... bei unveränderter Amplitude.
Das Übersetzungsverhältnis beim Transformator ist konstant. Der ideale Transformator speichert keine Energie. Die Flussverkettung ist ideal.
Wenn du weißt, was ein Transformator ist, fress ich ´nen Besen.
Du schmeißt leider Effekte der Selbstinduktion, der gespeicherten Energie in einer Spule und den Transformator, der im Idealfall keine Energie speichert, beliebig durcheinander, jonglierst damit und heraus kommen lauter falsche Annahmen.
Bei einem Transformator hängt die Übersetzung ausschließlich von der Windungszahl ab (Verhältnis der Windungszahlen, präziser) und nicht von der Frequenz (wenn du natürlich Gleichspannung versuchst....). Was hat das jetzt mit deiner zitierten schnellen Feldänderung zu tun? Ich denke, du sprichst von einem Transformator? Wer ändert denn dein "Feld" dort schnell?
Was meinst du mit: Das gilt jetzt in einer einzelnen Spule.... ? Ich denke, du stellst eine Frage zu einem Transformator?
Also: Dunkel war der Frage Sinn....
Wieso tue ich „erwachsen“? Ich habe die Frage mit meinen eigenen Worten formuliert und WAR der Meinung, ich wüsste was ein Transformator sei! Ich wollte lediglich, dass ich qualifizierte Antworten auf meine Frage erhalte, aber die Antworten von euch haben mein Gehirn komplett gesprengt und ich musste alles erstmal überdenken und mir ist aufgefallen, wie ihr schon gesagt habt, dass ich Spule und Trafo miteinander verglichen habe, was natürlich nicht so funktionieren kann.
Wie gesagt sie hat mit keinem Trafo experimentiert, sondern mit einer Spule. Aber wieso genau wird beim Trafo nicht das Magnetfeld vorgegeben?
Und wieso erzählt mir meine Lehrerin das? Dass die induzierte Spannung stärker ist umso schneller man das Magnetfeld verändert? In einer ganz normalen Spule! Das hat sie uns an einem Experiment sogar gezeigt
das stimmt ja auch ;-)
Trotzdem ist die induzierte Spannung beim TRAFO frequenzunabhängig.
Versuche mal deine Gedanken zu ordnen, du bringst alles durcheinander und vergleichst Äpfel mit Birnen ;-)
Du kannst deine Spulen-Experimente nicht auf den Transformator durch derartige Vergleiche übertragen. Das führt zu scheinbaren Widersprüchen.
Beim Trafo wird das Magnetfeld durch die eine Windung verursacht und dieses ist mit der anderen Windung wiederum verkoppelt - möglichst ideal. Ein Transformator überträgt von einer Windung zur anderen 1:1 mit dem Nutzen der Potenzialtrennung - wenn sie denn vorgenommen wird. Beim Spartrafo fällt selbst das weg. An jeder einzelnen Windung ist zur gleichen Zeit die gleiche Spannung. Egal, ob die Windungen miteinander galvanisch verbunden sind oder nicht. Egal, in wie viele Gruppen die Windungen verschaltet sein mögen.
Ich glaube kaum, dass deine Lehrerin den Versuch mit einem Transformator gemacht hat.
Wenn du deine Spule aus dem Unterricht z.B. bifilar gewickelt hättest, könntest du an beiden Teilwicklungen exakt dasselbe beobachten. Beim Trafo wird nicht das Magnetfeld vorgegeben, sondern an eine Wicklung eine Spannung angelegt - und diese wiederum wird induktiv verkoppelt (möglichst ideal durch gute Flussverkettung) auf jede andere Wicklung transformiert - stets 1:1 je Windung. Ziel des Transformator-Bauers ist es auch, die Streuinduktivität (also die eigene "Spulenwirkung" mit der darin gespeicherten magnetischen Energie) - möglichst gering zu halten, am liebsten zu null zu machen. Genau damit hatte aber deine Lehrerin offenbar experimentiert.
Wenn du weißt, was ein Transformator ist, fress ich ´nen Besen.
Er geht in die 10. Klasse...woher soll er das wissen?
Woher soll ICH das denn wissen?
Warum kann das hier nicht offen stehen, das ist doch völlig in Ordnung: "...Ich habe eine Frage, gehe in die 10. Klasse, und mir ist aufgefallen, dass...."
Warum tut er "erwachsen"? Ich nehme ihn ernst und dann kommt natürlich keine altersgerechte Beantwortung heraus, das tut mir Leid. Ich tauge nicht zum Lehrer für junge Schüler, sondern an der Hochschule.
Was heißt dunkel? Ja, ich gebe zu ich bin ein bisschen vom Thema abgekommen, aber ich hatte echt kein Bock das alles noch mal neu zu schreiben. Mit schnell meine ich, je schneller das Magnetfeld verändert wird, desto stärker ist die induzierte Spannung?!
Nein. Beim Trafo gilt das so nicht. Das Verhältnis von Ausgangs- zu Eingangsspannung ist dort konstant, solange der Transformator in seinem ausgelegten Bereich betrieben wird (nicht in der Sättigung).
Du kannst damit z.B. auch rechteckförmige Spannungen übertragen, deren Amplitudenverhältnis zueinander immer dasselbe bleibt, wie es bei sinusförmigen Größen ist.
Transformatoren werden im Prüffeld bei z.B. 4-facher oder 6-facher Netzfrequenz gemessen - zur Überprüfung der Auslegung. Ich habe dort Messprotokolle bei 200Hz und teils bei 300Hz für 50Hz-Netztrafos vorliegen. Das Übersetzungsverhältnis ändert sich nicht, es ist nicht frequenzabhängig, die Kurvenform der Spannungen wird (näherungsweise) nicht verändert.
Hier der Verlauf von I (blau) und Uind(rot) für
U=1 V
R= 1 Ohm
L = 1 H
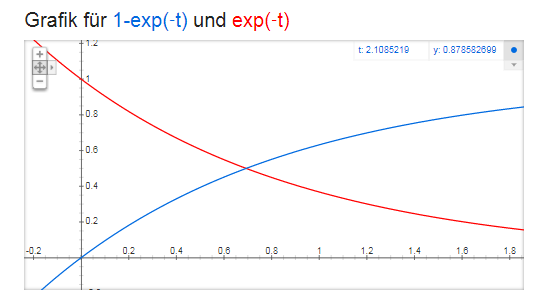
Ist ja quasi so wie in einer chemischen Gleichgewichtsreaktion fällt mir auf
Hier das Bild.
Abszisse: Zeit in s, Ordinate: Strom in A.
Einschaltvorgang für Spule.
L=1H
R=1Ohm
U=10V
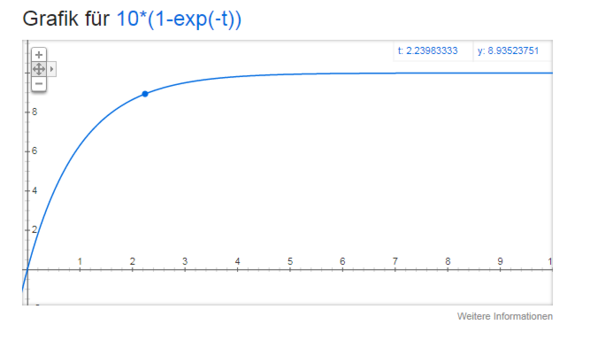
Kann es sein, dass der Grund ist, dass wir schon eine Anfangsspannung haben?