Funktion f konvergiert => Ableitung f' konverg. gegen 0?
Guten Tag [ oder Nacht :') ],
ich würde gern wissen, ob die Behauptung wahr ist, dass wenn eine Funktion f: IR -> IR konvergiert auch deren Ableitung gegen 0 konvergiert.
Wenn es sich um eine Funktion handelt, die ab einem gewissen Wert stets monoton ist, dann müsste die Aussage eigentlich relativ offensichtlich so wahr sein, wenn ich mich nicht irre.
Wenn es nun aber eine Funktion ist die zwar konvergiert, aber dabei oszilliert und deren "Wellenlänge" dabei proportional zur Amplitude abnimmt, stimmt die Aussage dann immer noch?
Die Frage kam mir relativ spontan in den Sinn, deshalb kann es sein, dass mein Gedanke unsinnig ist, aber ich würde mich über eine Antwort sehr freuen.
.
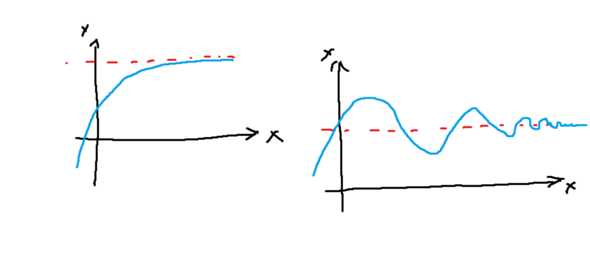
Kannst du mal eine Skizze hochladen
Hab es hinzugefügt so wie ich es ungefähr im Kopf hatte.
4 Antworten
Ja, genau deine Idee führt zum Ziel:
x^(-1/2) * cos(x^2) konvergiert gegen 0 für x -> inf.
Ableitung: -1/2 * x^(-3/2) * cos(x^2) + x^(-1/2)*sin(x^2) * 2x. Der erste Summand konvergiert gegen 0, der zweite nicht.
Perfekt, vielen Dank! Ich hatte damit gerechnet, wobei es mir eigentlich lieber gewesen wäre, wenn meine Vermutung falsch wäre :')
f(x) = (sin x²)/x beschreibt deine Funktion.
Die Ableitung davon konvergiert als 2 * cos x² - (sin x²)/x² nicht.
Zweite Antwort: Das gilt nicht einmal für monotone Funktionen.
Die Idee ist hier, zunehmend steilere Stufen einzubauen, die schneller steiler werden als die Funktion an sich abfällt.
Definiere erstmal eine "Verbindungsfunktion"; nennen wir die mal phi(x) mit folgenden Eigenschaften:
- phi ist auf dem [0,1] definiert.
- phi(0) = 0, phi(1) = 1
- phi ist mononton steigend
- phi ist differenzierbar
- phi'(0) = phi'(1) = 0.
Das Polynom phi(x) = (3-2x)*x^2 tut das zum Beispiel.
Beachte, dass mit phi auch phi^2, phi^3 etc. diese Eigenschaft haben.
Dann definiere g(x) folgendermaßen:
für x\in{n,n+1}, n jeweils die nächstkleinere ganze Zahl von x.
g hat folgende Eigenschaften:
- g ist monoton fallend gegen 0 für x->inf.
- g ist global differenzierbar
An den Intervallmitten x = m + 1/2 (mit m natürliche Zahl) gilt
g'(m+1/2) = (1/m - 1/(m-1)) * (phi'(1/2))^n.
Mit der Wahl von phi wie oben ist
phi'(1/2) = 3/2.
Damit ist
g'(m+1/2) = (1/m - 1/(m-1)) * (3/2)^n.
Der erste Faktor fällt wie 1/m, der zweite wächst exponentiell, das Produkt wächst damit unbeschränkt.
Damit haben wir eine Funktion konstruiert, die gegen Null geht, monoton und differenzierbar ist, deren Ableitung aber nicht gegen Null konvergiert.
Ich würde mit der Ableitung f' anfangen:
h(x) := 1/(x²+1) hat die Stammfunktion arctan(x). Stauche h für jedes k∈ℕ in x-Richtung um k² und verschiebe das um k nach rechts:
hₖ(x) := 1/(k²(x-k)²+1)
f'(x) := Σₖ hₖ(x) hat dann an jeder Stelle x=k eine Spitze größer als 1, die aber immer schlanker wird (siehe WolframAlpha)
Und das uneigentliche Integral f(x) := ∫ f'(x) dx ergibt einen „arctan mit Schluckauf“: An jeder Stelle x∈ℕ gibt es einen kleinen zusätzlichen Schub mit Steigung 1. In Summe bewirken diese Schübe aber nur, dass f gegen π (statt π/2) konvergiert.
ToDo: Zeige, dass f existiert und die Ableitung f' hat. Ich denke, dass die hₖ(x) so gutmütig sind, dass es dafür einen schönen Satz aus Analysis 1 gibt.
Ich muss zugeben, dass ich das nicht ganz nachvollziehen kann :') Ich hab zwar auch vergessen zu schlafen, aber das wird dabei nicht der maßgebliche Faktor dafür sein.
Ich habe mir auch kurz überlegt, wie ich eine monotone Funktion aufbauen würde, die konvergiert und deren Ableitung nicht gegen 0 konvergiert. Ich habe zumindest mal eine Idee, ob diese stimmt weiß ich leider nicht.
Das ist jetzt eine dumme Frage und ich kann jetzt gerade leider nicht im Skript schauen, aber muss eine differenzierbare Funktion (wie hier phi) nicht immer auf einer offenen Definitionsmenge definiert sein?
Nochmals Danke für die Mühe!
Ja, ich hätte schreiben sollen, "differenzierbar auf (0,1)" (dem offenen Intervall). Definiert sein muss sie aber für meine Zwecke zumindest auf dem einseitig abgeschlossenen Intervall, da sonst die von mir konstruierte Funktion g Lücken hätte.
Naja, wie ich geschrieben habe: Die Idee ist schon korrekt, aber das Beispiel ist kompliziert. Mein Bauchgefühl sagt mir, dass es da was Einfacheres gibt, aber ich habe das noch nicht gefunden!
Deine Gedanken sind so richtig. Eine Funktion die monoton steigt oder fällt und gegen einen Wert konvergiert, hat eine Ableitung die gegen 0 konvergiert.
Für oszillierende Funktionen ist dies nicht zwangsweise der Fall. Gutes Beispiel hier sind gedämpfte Schwingungen.
Deine erste Aussage über monotone Funktionen ist so nicht richtig, siehe meine zweite Antwort.
Deine zweite Aussage ist richtig, aber eine gedämpfte Schwingung ist kein gutes Beispiel, da die Frequenz sich ja nicht ändert, und das brauchst du, damit die Ableitung unbeschränkt wird.
(PS: Wenn mir ein einfacheres Beispiel einfällt, schreibe ich das auch noch hier hinein...)