Mathe Thema: Funktionsuntersuchung 10. Klasse?
Ich habe Aussagem bekommen bei denen ich sagen muss ob sie wahr oder falsch sind (ES SIND KEINE HAUSAUFGABEN, ES SIND LEDIGLICH AUFGABEN FÜR MICH VOM LEHRER, ABER ICH MUSS SIE DEM LEHRER NICHT ZEIGEN) Ich bin mir bei folgenden Aussagen unsicher
1. Zwischen zwei benachbarten Extrempunkten auf dem Graphen von f liegt immer ein Schnittpunkt mit der x- Achse
2. besitzt eine ganzrationale Funktion vierten Grades genau zwei hochpunkte und ein tiefpunkt so ist der Graph ihrer zweiten Ableitung eine nach oben geöffnete Parabel
3.eine ganzrationale Funktion sechsten Grades kann höchstens 5 extrempunkte besitzen
4.besitzt die Ableitung einer Funktion f genau drei nullstellen, so besitzt die Funktion f genau drei extremstellen
Ich hoffe ihr könnt mir helfen. ( ICH WIEDERHOLE; ES HANDELT SICH NICHT UM HAUSAUFGABEN) + es wäre nett wenn ihr das begrümdet muss aber nicht sein, weil ich es mir vielleicht dann selbst erschliessen kann, aber bis jetzt versteh ich diese Aussagen nicht wirkkich.
3 Antworten
1.: f(x) = x^3 - x + 5
2.: such dir ein beliebiges Beispiel raus
(zwei Hochpunkte und ein Tiefpunkt - der dann zwischen dren beiden Hochpunkten liegt - bedeuten, dass die Funktion für x-> plusminus unendlich gegen - unendlich geht. Das Vorzeichen der Ableitung ist bei Polynomen für genügend große Argumente dasselbe wie das der Funktion selbst, bei negativem Argument multipliziert mit (-1)^n (oder die Ableitung ist konstant 0).
3.: Die maximale Anzahl der Nullstellen eines Polynoms ist gleich dem Grad des Polynoms. Der Polynomgrad verringert sich beim Ableiten um 1.
4.: Es gibt auch Sattelpunkte (Wrndepunkte mit waagerechter Tangente)
Meiner Meinung nach:
- falsch (Beispiel wurde hier gepostet)
- richtig (Zwei HP und 1 TP heißt f nach unten geöffnet, also f' von +unendlich nach -unendlich gehend, also f'' zunächst im Negativen und dann im Positiven, also nach unten geöffnete Parabel)
- richtig (f' hat dann max. 5 Nullstellen, also f max. 5 Extremstellen)
- falsch (f hat MAX. so viele Extremstellen wie f' Nullstellen, aber nicht zwingend genauso viele)
Guten Abend!
Ich weis jetzt nicht wie weit ihr schon in Mathe seid.
Aber zu 1. möchte ich dir gleich mal ein Beispiel zeigen
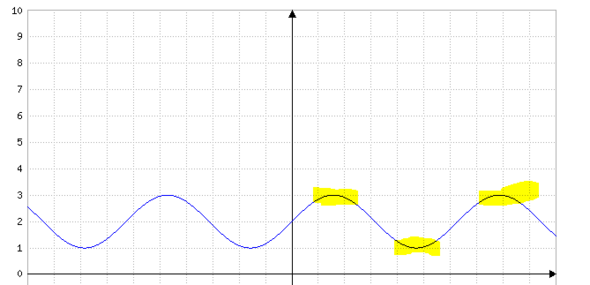
f(x)=sin(x)+2
Die Funktion besitzt unendlich viele Extremstellen (Hoch und Tiefpunkte), jedoch keinen Schnittpunkt mit der x-Achse.
Ergo existiert kein Schnittpunkt mit der x-Achse zwischen beliebig vielen Extrempunkten
2-4 erkläre ich dir morgen bei Bedarf....müüüüüde ;)
