Beweis/Grund für Einsetzen eine Extremstelle in 2. Ableitung
Bei einer ganzrationalen funktion setzt man ja die erste Ableitung Null um die Stelle des EPunktes zu berechnen. Um dann zu berechnen ob es ein Hoch oder Tiefpunkt ist, setzt man die Stelle des EPunkts in die 2. Abgleichung ein. Ist der Funktionswert größer als 0 hat man einen TP ist er kleiner hat man einen HP.
Wieso man den EP mit der ersten Ableitung ermittelt haben die meisten meiner Freunde mit dem Übereinanderlegen der Graphen heraus gefunden. Vllt kann man ja auch so meine Frage beantworten.
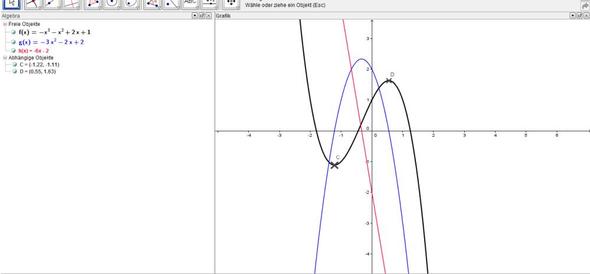
Ich hab mal ein Beispiel hinzugefügt
3 Antworten

Zu der guten Erläuterung von ultrarunner möchte ich noch eine Anschaulichkeit hinzufügen. Nachtfahrer hat ja auch schon vermerkt, daß eine negative zweite Ableitung eine Rechtskurve und eine positive 2 Abl. eine Linkskurve darstellt.
Das kann man sich auch so verdeutlichen (und merken): Eine Rechtskurve zeigt in ihrem Gesamtverlauf nach Unten - also negativ; der Funktionsgraph steigt zwar vor dem Hochpunkt noch an, aber die Steigung verringert (--> negativ) sich ständig bis sie Null ist (Hochpunkt) und von da an geht es bergab und zwar mit zunehmender negativer Steigung.
Bei einer Linkskurve das gleiche nur eben anders rum; sie steigt im Gesamtverlauf (also positiv).
Das sind nicht nur spinnerde Überlegungen von Mathematikern, sondern werden im "täglichen" Leben benutzt und habe eine wichtige Bedeutung. Z.B. die Aussage "die Inflation steigt oder fällt" bezieht sich auf die 2.Ableitung der Geldwertfunktion. Inflation heißt ja schon mal, daß das Geld an Wert verliert, also eine fallende Funktion. Wenn die Inflation steigt, dann wird der Verlust immer stärker, die Geldwertfunktion befindet sich in einer Rechtskurve, also 2.Abl negativ. Politiker freuen sich immer, wenn sie von sinkender Inflation berichten können, das klingt zwar gut, heißt aber nur daß die 2.Abl poitiv ist, also der Geldwertverlust nicht mehr so stark ist; das Geld verliert trotzdem weiterhin an Wert.
Und daß es in der Physik (z.B. Luftfahrt, Raumfahrt, etc.) wichtig ist ob eine Kurve nach oben oder unten geht, z.B. bei einer Messung ist ja auch vollkommen einleuchtend. Also diese Überlegeungen wie die 2.Abl aussieht ist schon sehr wichtig und hilft sehr bei der Interpretation von Funktionen.

Dunkel erinnere ich meine Schulzeit ... Da stellte sich (also der Lehrer der Klasse) die Frage, wie denn wohl eine Tangente an einem Punkt P einer Kurve zu ermitteln sei. Eine Tangente geht durch einen Punkt und hat eine Steigung, ist damit vollständig bestimmt. Der Punkt ist schon mal da - P halt. Braucht's noch die Steigung - und einen Punkt P', der 'ziemlich nah' an P liegt, dann ist die Steigung ja schon 'ziemlich gut' bestimmt - und ganz genau, wenn man P' strückchenweise zu P hin wandern lässt, eine grenzwertige Betrachtung. - Anschaulicher wird's, nimmt man 2 Punkte, P' und P'', beidseitig von P, und lässt diese gemeinsam zu P hin wandern - zeichnerisch 'näher', rechnerisch aber komplizierter, und daa tut's ein P' ja auch ...
Das Wunder geschah, die 1. Ableitung war abgeleitet - und klar: die 'Steigung' in einem EP muss ja ...
Nun gibt es ja dieverse 'Kurven', und die haben Eigenschaften - u.a. die, dass sie gebogen sind, und da gibt's 2 Möglichkeiten: rechts eröm oda links eröm (mathematisch: positiv/negativ), und dann gibt's da noch sowas wie 'Radius' ... Was das nun wieder (mathematisch) mit der 2. Ableitung zu tun hat, ist meinem Gedächtnis entschwunden, hängen blieb nur dass .. Nullstellen der 2. Ableitung führen entsprechend zu 'Wendepunkte'n.

Eine Ableitung gibt immer die Steigung der Tangente an die abgeleitete Funktion an. Schließlich hat man sie ja genau so definiert (siehe Kapitel "Einführung in die Differentialrechnung").
Wenn du dir den Graphen einer beliebigen Funktion mit Extremstelle ansiehst, wirst du bemerken, dass Extremstellen immer eine waagrechte Tangente haben - d.h. eine Gerade mit der Steigung 0. Deshalb kann man Extremstellen finden, indem man die Ableitung der zu untersuchenden Funktion 0 setzt.
Leitet man nun die Ableitung wieder ab, erhält man eine Funktion, welche die Steigung der Ableitung liefert. Bezogen auf die ursprüngliche Funktion handelt es sich dabei um die Krümmung.
Wenn du dir den Graphen einer beliebigen Funktion mit Extremstelle ansiehst, wirst du bemerken, dass an einem Hochpunkt die Krümmung immer negativ ist, und an einem Tiefpunkt immer positiv. Aus diesem Grund kann man die Art einer Extremstelle finden, indem man die zu untersuchende Stelle in die 2. Ableitung einsetzt.