Fourier Transformation von f(x)=x in [-1;1]? Wie berechne ich das?

Hallo, wie würde man die Fourier Transformation von f(x)=x berechnen, mit den Grenzen -1 bis 1?

Die Formel müsste ja

$\frac{1}{\sqrt{2\ \pi}}\cdot\int_{-1}^1x\cdot e^{-i\ \omega x}dx$ sein.. Nur von da komme ich um ehrlich zu sein nicht weiter. Ich hatte es zuerst versucht mit der partiellen Integration mit u=x und das funktioniert auch an sich, aber ich bin mir einfach nicht sicher ob ich das ganze richtig berechnet habe, da ich zu der Aufgabe keine Lösung habe.

Comments

[Halbrecht]

was ist die Funktion x x ?

vielleicht kein Respekt der Korrektur für die Antworterinnen ?

[niklol]

Entschuldigt, die funktion ist f(x)=x

Answer 1

[Rammstein53]

Es ist einfacher, die reelle Fouriertransformation anzuwenden mit den Koeffizienten a(k) und b(k), k € N0 (Formel bitte im Internet suchen).

Wegen f(x) = -f(-x) sind alle Koeffizienten a(k) Null. Damit entfallen alle cos-Anteile.

Für b(k) gilt:

$b\left(k\right)\ =\ \int x\cdot\sin\left(pi\cdot x\cdot k\right)\ dx$

Integriert wird über das Intervall [-1,+1]. Die ersten b(k) lauten

b(1) = 2/pi

b(2) = -1/pi

b(3) = 2/(3*pi)

b(4) = -1/(2*pi)

b(5) = 2/(5*pi)

b(6) = -1/(3*pi)

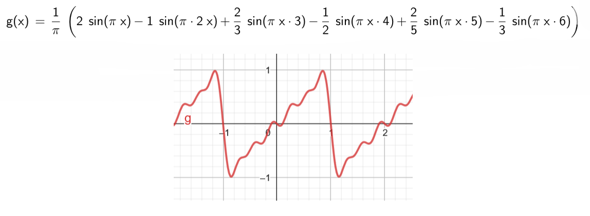
Die Fourierreihe sieht dann so aus:

$\sum_{k=1}^nb\left(k\right)\ \cdot\ \sin\left(pi\cdot k\cdot x\right)$

Mit diesen ersten 6 Koeffizienten ergibt sich folgendes Bild: