Extremwertaufgabe?
Servus,
ich brauch Hilfe bei folgender Extremwertaufgabe:

Bitte um ausführliche Erklärung.
2 Antworten
Hallo,
wegen der Achsensymmetrie betrachtest Du nur die rechte Seite des Dreiecks, das von x=0 bis x=3 geht.
Die Funktionsgleichung der Seite, die vom y-Achsenabschnitt bei 8 bis zur Nullstelle bei x=3 geht, kannst Du praktisch ablesen. Sie lautet y=8-(8/3)x, denn auf drei Einheiten nach rechts in der Waagerechten verliert sie 8 Einheiten nach unten.
Das halbe Rechteck hat somit die Fläche x*(8-(8/3)x), also Breite mal Höhe, wobei die Höhe von x abhängig ist - die rechte obere Ecke des Rechtecks liegt auf dem Dreieck.
Ausmultiplizieren: 8x-(8/3)x²
Nach x ableiten: 8-(16/3)x.
Ableitung gleich Null setzen und nach x auflösen ergibt x=3/2.
x=3/2 in die Geradengleichung einsetzen ergibt 4.
Das Rechteck hat also eine Breite von 2*3/2 (es erstreckt sich ja auch links der y-Achse) und eine Höhe von 4.

Herzliche Grüße,
Willy
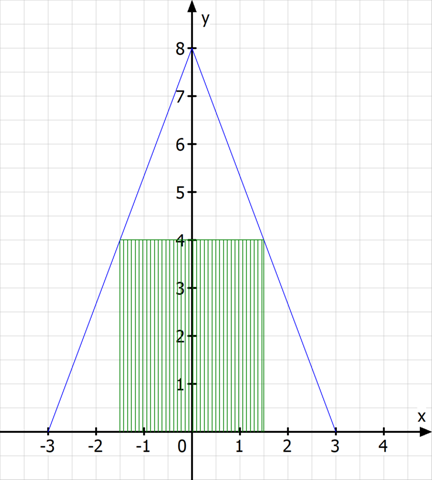
Spoiler: genau halbe Höhe und halbe Breite
Für einen langen Vortrag über Extremwertaufgaben reicht meine Zeit gerade nicht.
Ach Willy leider hast du hier deine Zeit vergeudet, schau dir mal die Kommentare vom Author an... Dieser hat leider nichts gelernt, ist beleidigend und steht bei der nächsten HA wieder hier. LG