Das Volumen berechnen von diesem Werkstück?
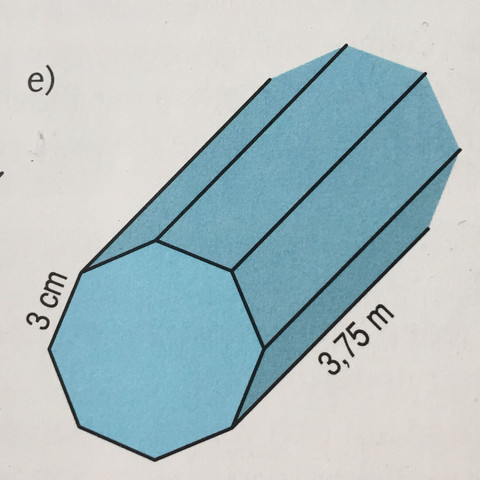
Wie kann ich das Volumen dieses Werkstücks (Bild) berechnen, was für eine Formel brauche ich. Das Thema lautet "Trigonometrie - Berechnungen an Körpern"
8 Antworten
Hallo,
es handelt sich um ein Prisma, in dem zwei regelmäßige Achtecke mit je 3 cm Kantenlänge durch parallele 3,75 m lange Strecken miteinander so verbunden sind, daß sie sich in zwei parallelen Ebenen befinden und senkrecht übereinander stehen. Somit muß die Höhe des Prismas schon mal nicht berechnet werden, sondern ergibt sich aus der Aufgabenstellung: 3,75 m oder
375 cm.
Das Volumen eines Prismas berechnet sich aus Grundfläche mal Höhe.
Die Höhe ist klar, die Grundfläche besteht aus acht gleichschenkligen Dreiecken, die alle gleich groß sind und deren Basis 3 cm lang ist.
Zu berechnen wäre nun die Länge der jeweiligen Schenkel bzw. die Höhe, also die Entfernung vom Mittelpunkt des Achtecks zu einer der Basisseiten.
Bekanntlich berechnet sich die Grundfläche eines Dreiecks nach der Formel:
Halbe Grundseite mal Höhe.
Da es sich um acht Dreiecke handelt, ist dann die Gesamtfläche des Achtecks 4 mal Grundseite mal Höhe. 4 mal Grundseite sind 12 cm. Das multipliziert mit der Länge der Höhe ergibt die Achtecksfläche, diese wiederum mit 375 cm multipliziert ergibt das Volumen des Prismas.
Das Achteck entsteht, wenn Du einen Kreis in acht gleich große Sektoren aufteilst und deren Enden durch gerade Strecken verbindest.
Der Mittelpunktwinkel jedes der acht Dreiecke läßt sich nun ganz leicht berechnen. Ein Vollkreis hat 360°. Teilst Du ihn in acht gleich große Abschnitte auf, ergibt der einzelne Winkel 360/8=45°.
Da sich die Winkel eines ebenen Dreiecks immer zu 180° ergänzen, bleiben für die beiden Basiswinkel demnach 180-45=135° übrig, womit auf einen Basiswinkel somit 135/2=67,5° entfallen.
Wenn Du eine Seite und drei Winkel in einem Dreieck hast (nur zwei Winkel geht nicht, denn wenn Du zwei Winkel hast, kennst Du auch den dritten), bietet sich der Sinussatz an, der besagt, daß sich in einem beliebigen Dreieck Seite und Sinus des gegenüberliegenden Winkels stets gleich verhalten.
Somit verhalten sich 3 cm zum Sinus von 45° genau wie x cm (die Länge eines Schenkels) zum Sinus von 67,5°.
Hast Du aber den Schenkel und die Grundseite, läßt sich die Höhe ganz einfach nach dem Satz des Pythagoras berechnen.
Die Katheten sind die gesuchte Höhe und die halbe Basisseite, die Hypotenuse ist der nach dem Sinussatz errechnete Schenkel.
Mit diesen Hinweisen solltest Du es eigentlich schaffen.
Viel Erfolg,
Willy
Du kannst Dir auch die Berechnung des Schenkels sparen, da Du für die Flächenberechnung des Dreiecks nur noch die Höhe benötigst. Die kannst Du über den Tangens berechnen:
tan (22,5)=(a/2)/h, also h=(a/2)/tan (22,5)
Die 22,5 kommen dadruch zustande, daß die Höhe den Winkel von 45° halbiert.
Da die Fläche eines Dreiecks h*a/2 ist und h hier a/(2*tan (22,5)),
kommst Du auf die Formel a²/(4*tan (22,5)) für die Dreiecksfläche.
Da es sich um acht Dreiecke handelt, berechnest Du die Achteckfläche nach der Formel F=2a²/tan (22,5)
Willy
Das Volumen ist Grundfläche x Höhe. Die Grundfläche besteht aus 8 Dreiecken mit dem Winkel 360° / 8 = 45° Jedes Dreieck besteht aus zwei rechtwinkligen Dreiecken mit einem Winkel von 22,5° und einer Hypothenuse in Länge des Radius. Mithilfe der Winkelfunktionen kannst Du auf dieser Basis die Höhe Und die Länge der Grundlinie (=Sekante im Kreis, der das 8-Eck umhüllt) der 8 gleichschenkligen Dreiecke ausrechnen.
Grundlinie x Höhe / 2= Fläche eines der acht Dreiecke. Mit 8 multiplizieren und der Länge des Achtkantstiftes und schon hast Du das Volumen.
Ein wenig kompliziert oder? Ein Oktogon hat eine Formel zum berechnen. Die ist
A = a2 (2+2 -/2)
a ist die Seite 3 cm die zwei dahinter will eine hoch zwei sein und das -/2 ist eine zwei unter einer Wurzel.
Hallo polishtumblrboy,
es handelt sich um ein Prisma, dessen Volumen gleich Grundfläche mal Höhe ist. Die Grundfläche ist ein regelmäßiges 8-Eck, dessen Seitenlänge gegeben ist. Die Höhe ist auch gegeben. Also wird es nicht so schwer sein. Ich erhalte zum Vergleich V = 16295,94 cm^3.
Gruß von leiermann
Da ist wohl ein Zylinder mit 8-eckiger Grundfläche gemeint. Möglicherweise ist noch gedacht (aber nicht wirklich ersichtlich), dass diese Grundfläche regelmäßig sein soll. Die Lösung könnte man sogar ohne Trigonometrie ermitteln.
Fläche des Boden (Achteck) mal Länge.
Auf die Einheiten achten.