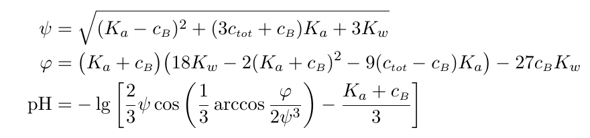[Chemie] pOH-Wert der Lösung berechnen?
Guten Nachmittag,
ich benötige noch ein bisschen Hilfe, um die folgende Aufgabe zu verstehen. Ich freue mich sehr auf eure hilfreichen Antworten 🙋♂️

- Woran erkenne ich hier überhaupt, dass es sich um eine Lösung eines schwachen konjugierten Säure-Basen-Paars handelt?
- Wenn ich das erkennen würde, würde ich wissen, dass ich mithilfe der Henderson-Hasselbalch-Gleichung den pH-Wert bestimmen kann und dann den pOH-Wert (pH + pOH = 14).
- Henderson-Hasselbalch-Gleichung: pH = pKs + lg([A^(-)]/[HA])
- Weiter komme ich hier aber noch nicht
1 Antwort
Du hast hier das Anion (=Base) und das Zwitterion (=Säure). Daß die beiden ein Säure/Base-Paar bilden, erkennt man dadurch, daß sich ihre Strukturen nur um ein H⁺ unterscheiden, es handelt sich also um das Gleichgewicht
RCH(N⁺H₃)CO₂¯ ⟶ H⁺ + RCH(NH₂)CO₂¯
das durch den pK₂ beschrieben wird.
Also ist es naheliegend, die Henderson–Hasselbalch-Gleichung anzuwenden:
pH = pK₂ + lg(Base/Säure) = pK₂ + lg(Anion/Zwitterion) = 9.1+lg(0.5/0.005) = 11.1
Das wäre auch schon die richtige Lösung, wenn die angegebenen Konzentration (0.5 bzw. 0.005 mol/l) die Gleichgewichtskonzentrationen der beiden Ionen wären. Vermutlich ist es aber gemeint, daß man die beiden Substanzen in diesen Konzentrationen einwiegt und sich dann erst das Gleichgewicht einstellt. Oft kann man diesen Unterschied ignorieren, aber hier spielt er doch eine gewisse Rolle, weil laut dem oben berechneten Resultat c(OH¯)=10¯ᵖᴼᴴ=0.0013 mol/l und daher nicht wesentlich kleiner ist als die Konzentration der Puffersubstanz selbst (Zwitterion, 0.005 mol/l). Daher muß man damit rechnen, daß das Resultat ungenau ist.
Wie kann man es genauer rechnen? Die Verbesserung der HH-Gleichung ist die Charlot-Gleichung, die man in mehreren Formen aufschreiben kann; ich bevorzuge die folgende:

Dabei bedeuten cₜₒₜ=0.505 mol/l die kombinierte Konzentrationen der Pufferspezies und cB=0.5 mol/l die basische Form. Das Resultat ist dann pH=11.02, es ist also nur eine kleine Korrektur die man vielleicht ignorieren kann.
Weiters haben wir das pK₁ vernachlässigt, aber das ist unproblematisch, weil es so viel kleiner ist als das pK₂. Bei einem pH rund um 11 ist die erste Dissozitionsstufe (das Gleichgewicht zwischen Kation und Zwitterion) so gut wie vollständig dissoziiert; eine genaue Rechnung ergibt übrigens c(Kation)=5⋅10¯¹² mol/l, c(Zwitterion)=0.006 mol/l und c(Anion)=0.499 mol/l im Gleichgewicht.
Wenn Du Deinen Lehrer ärgern willst, dann sagst Du ihm das richtige Resultat pOH=3.0, wenn Du mit Konformität schleimen willst dann reichen auch 2.9 — Deine Entscheidung.